-
Les trois médiétés de la théorie classique
LES TROIS MEDIETES DE LA THEORIE CLASSIQUE
A la fin de son Introduction arithmétique, et comme en couronnement de ce livre, Nicomaque qualifie de "médiété parfaite" la série harmonique (6 - 8 - 9 - 12), dont l'importance dans la mathématique pythagoricienne est telle, qu'elle a reçu le nom de "grande tétractys". Récemment, certains auteurs se sont même enthousiasmés à voir en elle la tétractys la plus ancienne ou la plus originelle, mais ces hypothèses historiques, au demeurant aussi gratuites que possible, n'ont pas d'intérêt pour les véritables pythagoriciens, puisqu'on a vu que cette grande tétractys n'était qu'une simple application, qu'un simple développement mathématique de la tétractys « classique ».
La perfection de la série harmonique (6 - 8 - 9 - 12), tient à ce qu'elle contient les rapports des trois médiétés que la tradition définit comme "premières en naissance"; et l'on sait déjà l'importance de ce critère en pythagorisme. Cet article sera consacré à illustrer cette primauté généalogique des trois premières médiétés sur les suivantes; et nous verrons au passage comment elles se déduisent de la série harmonique de la grande tétractys. On s'efforcera ensuite, dans les deux articles suivants, de traiter du système complet des médiétés.
Comme la théorie du gnomon, l’étude du système des médiétés est un domaine encore peu exploré de la mathématique. Le nombre même de ces médiétés est une question problématique, et fait l’objet d’un flottement selon les auteurs : 10 selon Nicomaque de Gérase, 12 selon Théon de Smyrne, 11 pour la plupart des auteurs récents qui ont tenté de donner une définition moderne de ce système. Nous montrerons ici que la détermination exacte du nombre des médiétés dépend de l’ensemble arithmétique dans lequel on les définit. En effet, s’il y a bien 11 médiétés dans N* (l’ensemble des entiers naturels, sauf zéro), il y en a 12 dans N (l’ensemble des entiers naturels, inclu zéro), conformément à la conjecture de Théon de Smyrne. Dans cette étude, on appelle « Nicomaque 1 à 10 » les 10 médiétés recensées dans le catalogue de cet auteur, et « Théon 11 et 12 » les deux qui ont dû leur être ajoutées. Nous donnons, à la fin de cette première section, une table des médiétés, à laquelle le lecteur pourra se reporter selon ses besoins.
En réalité, seules les trois premières de ces médiétés, qui sont les médiétés immédiatement déductibles des rapports arithmétiques de la grande tétractys, ont fait l’objet, - et ce, dès l’antiquité - d’une étude vraiment détaillée. A ces trois médiétés classiques on peut ajouter la médiété Nicomaque 10, qui a fait l’objet d’un intérêt plus récent, en raison de sa relation avec la célèbre « suite de Fibonacci ».
*
Définitions
René Taton.
"Une médiété est un rapport entre trois termes, tel que deux d'entre eux et deux de leurs différences soient dans le même rapport."
Cette définition peut être transformée en une définition purement logique et formelle, sans contenu sémantique. Par exemple :
Une médiété est une expression à six places vides de la forme ci-dessous, dans laquelle les relations arithmétiques entre les termes sont constantes, et où les six places doivent être remplies par les lettres a, b, c, telles que a < b < c.
(...) - (...) = (...)
(...) - (...) (...)
Enfin, les relations arithmétiques entre les termes étant supposées connues, il est possible, comme nous le verrons dans la partie démonstrative de cet exposé, de réduire le problème des médiétés à celui d'un tableau à six cases (logon), où les cases doivent être remplies par les lettres a, b et c.
a
a
a
a
a
a
De telles définitions ne sont bien sûr pas complètes, puisque, si toutes les médiétés sont des expressions de cette forme, toutes les expressions de cette forme ne sont pas des médiétés. En effet, le total des solutions possibles pour cette formule est de 36 = 729, entre lesquelles un petit nombre seulement, de dix à douze selon les auteurs, sont des médiétés.
Nous appellerons ici mineure la partie de l'expression située à droite du signe égal, concernant des termes simples (a, b, ou c) et majeure celle située à gauche du signe égal, concernant des différences entre ces termes, et conviendrons de placer toujours la majeure devant la mineure, comme ci-dessus.
Nous présenterons les 6 premières médiétés dans leur ordre traditionnel, qui est d'ailleurs l'expression d'une réalité structurelle que nous traiterons en son lieu. La documentation sur les 3 premières médiétés est assez abondante, et, ne pouvant les traiter de façon exhaustive, nous favoriserons ici, en fonction des besoins qui sont les nôtres, d'une part, les éléments de description qui permettent d'extraire des médiétés un contenu intuitif ou intellectif, d'autre part, les éléments permettant de dégager les aspects topologiques et structurels du système des médiétés.
Comme il n'entre pas dans notre propos d'étudier la place des médiétés dans l'histoire de la philosophie, on se contentera, ici, de citer quelques exemples. Platon, dans le Timée, recourt à la médiété géométrique pour construire son échelle harmonique de l'âme du monde. Aristote, dans son Ethique à Nicomaque, utilise la même médiété pour exposer le principe économique de la justice et de l'égalité. Fibonacci montre, lui, comment on peut utiliser la médiété 10 pour décrire la croissance d'une population de lapins; et c’est un peu dans le même esprit que Malthus, dans son célèbre théorème économique, énonce que la population humaine s'accroît en moyenne géométrique, alors que ses ressources ne s'accroissent qu'en moyenne arithmétique.
Evoquons une question de vocabulaire. L'usage d'appeler "arithmétique", "géométrique" et "harmonique" les 3 premières médiétés est traditionnel. Il est déjà présent chez Archytas, et a même reçu chez Nicomaque une justification étendue. Quelle que soit l'ancienneté de cet usage, il nous paraît, à nous, plutôt de nature à engendrer la confusion. Les 3 médiétés renferment chacune des aspects arithmétiques, géométriques et harmoniques; ces appellations ne sont donc pas décisives pour comprendre leurs propriétés principales, du moins au point de vue qui est le nôtre.
Bien que la tradition attribue à Pythagore la découverte des 3 premières médiétés, la première recension écrite de ces médiétés se trouve dans l'oeuvre d'Archytas de Tarente. Pour ces trois médiétés, nous donnerons à chaque fois en ouverture la définition d'Archytas.
La médiété arithmétique
Archytas :
"En musique, il existe trois médiétés : arithmétique, géométrique et subcontraire, encore appelée harmonique.
"On parle de moyenne arithmétique, quand trois termes entretiennent entre eux une proportion selon un excès donné, et que l'excès du premier par rapport au deuxième est celui du deuxième par rapport au troisième."
Précisons que nous suivons ici l'usage moderne, de préférence à celui d'Archytas, et désignons comme "le premier" (a) le plus petit des trois termes, et appelons "c", ou "troisième", le plus grand des trois termes.
Cette médiété se note :
b - a = a ( = b = c ) ( = 1)
c - b a b c
avec : a < b < c
Et sa plus petite solution possible pour (a, b, c) est (1, 2, 3)
L'exemple le plus simple que l'on puisse trouver est donc celui de la suite des entiers naturels : 1, 2, 3, 4, 5, ....
Commençons par détailler quelques propriétés de cette médiété.
On a :
c - b = b - a
b = a + c
2
c = (b - a) + b
c = 2b - a
Si l'on prend la chaîne des entiers naturels, on constate que l'on peut appliquer à n'importe quel endroit de cette chaîne un objet logique en forme de trident, correspondant aux termes a, b, c; en vertu de quoi tout triplet de nombres successifs choisis dans cette chaîne satisfait la médiété "Nicomaque 1", ou médiété "arithmétique".
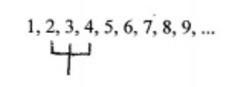
Mieux encore, cet objet logique, le trident, peut être affecté d'un vecteur de croissance indéfinie, de manière à pouvoir sélectionner cette fois des termes non voisins de la chaîne, à la seule condition que la croissance du trident soit uniforme, c'est-à-dire, que l'égalité entre les deux sous-intervalles soit continuellement maintenue.

Résumons les aspects les plus originaux de la médiété arithmétique.
- Dans cette médiété, le rapport mineur a une valeur constante : 1. Cette particularité est propre à la médiété Nicomaque 1 à l'exclusion de toutes les autres.
- Dans sa solution la plus simple (1, 2, 3), cette médiété a une signification intuitive qui est l'opération "+1", qui engendre la chaîne des entiers, et qui est aussi l'explication de son qualificatif d'arithmétique.
- Dans son application par la croissance du trident, cette médiété a une signification intuitive qui est la continuité, à toutes les échelles du nombre, de la fonction d'intervalle régulier. La croissance du trident est tout simplement la croissance endomorphe de la fonction arithmétique d'intervalle régulier, qui, partant d'une portion atomique ou entière d'intervalle, s'étend ensuite, par une progression continue, à toutes les dimensions pouvant contenir celle-là, comme une partie. A partir d'un intervalle minimum, sommet d'un cône topologique, est défini le principe de la croissance illimitée de cet intervalle.
- Ajoutons une dernière singularité. La médiété Nicomaque 1 est la seule à comporter 3 fractions du côté de la mineure. Une autre médiété, la médiété Nicomaque 2, comporte 2 fractions, tandis que les dix autres ne comportent qu'une seule fraction.
Ces précisions nous serons utiles lorsque nous aurons à analyser le sous-système constitué par les 3 premières médiétés.
La médiété géométrique
Archytas :
"On parle de moyenne géométrique, quand le rapport des trois termes est tel que le premier est au deuxième ce que le deuxième est au troisième."
Des exemples courants de cette médiété sont les proportions que nous appelons communément "double", "triple", "quadruple", etc.
Ainsi, la série suivante (double) :
1, 2, 4, 8, 16, 32, 64, 128, ...
Ou encore la série suivante (triple) :
1, 3, 9, 27, 81, 243, ...
On voit que le domaine d'application de cette médiété est, comme celui de la précédente, d'une grande généralité mathématique, puisque les rapports tels que "double", "triple", dont la liste est évidemment infinie, peuvent, chacun à son tour, être appliqués à tout nombre n, comme on vient de le faire ici au seul nombre 1.
Cette médiété se note :
b - a = a ( = b )
c - b b c
et sa plus petite solution possible pour (a, b, c) est (1, 2, 4).
Pour cette médiété, on a, outre la définition d'Archytas, celle du Timée de Platon.
(On parle de moyenne géométrique), "chaque fois que, de trois nombres quelconques, que ces nombres soient entiers ou en puissance, celui du milieu est tel que ce que le premier est par rapport à lui, lui-même l'est par rapport au dernier, et inversement, que ce que le dernier est par rapport à celui du milieu, celui du milieu l'est par rapport au premier, le dernier et le premier pouvant à leur tour devenir moyen."
C'est cette médiété qui sera mise en oeuvre ensuite dans la célèbre construction arithmétique et musicale de l 'âme du monde
Nicomaque, quant à lui, nous introduit à cette médiété par une voie apparemment détournée, qui est de la considérer d'abord comme un problème à 4 termes, pouvant ensuite être ramené à 3 termes. Cette voie d'exposition étant assez intellective, nous nous y attarderons un instant.
Si nous considérons des séries familières telles que les rapports : « double », « triple », etc :
1, 2, 4, 8, 16, ...
1, 3, 9, 27, ...
On observe que :
a/b = c/d = e/f = ...
Ce qui, pour la série double, donne :
1/2 = 4/8 = 16/32 = ...
Et pour la série triple :
1/3 = 9/27 = 81/243 = ...
Si nous exprimons maintenant cette application comme une fonction "en trident", cela revient à dédoubler la barre centrale du trident, de façon à inclure désormais quatre termes dans la relation, soit :

Où : 1/2 = 4/8 = ...
La médiété devient alors une fonction qui relie des termes successifs par paires, exprimant que chacune des fractions composées d'une de ces paires est égale à la suivante et à toutes les suivantes.
Mais n'oublions pas que le rapport "trident" qui est présenté ci-dessus sous une forme "disjointe", peut être ramené à une forme "conjointe", donc à un trident simple, puisque la proportion qui court dans les intervalles - les "trous" de la chaîne ci-dessus - est également la même. En effet :

Les rapports : 2/4, 8/16, ..., correspondant à ces "jointures" supérieures sont eux mêmes égaux à ceux de la chaîne inférieure.
Notons qu'à partir d'une suite de termes étendue telle que :
a b c d e f g h
on peut former des équations telles que : a/d = e/h, ou encore a/c = b/d. Les segments peuvent croître indéfiniment, ou se croiser, pour peu qu'il soient toujours de même longueur.
Pour conclure, remarquons une propriété de cette médiété, qui peut éclaicir le contenu sémantique de celle-ci; de la même manière que nous avions reconnu dans la première médiété un contenu sémantique qui est la constance, à toutes les échelles du nombre, de la fonction d'intervalle régulier.
Dans cette médiété, on a : ac = b2
par exemple 1 x 4 = 22, etc, dans la série "double".
ou 1 x 9 = 32, etc, dans la série "triple".
Une façon de comprendre cette médiété peut donc consister à transformer l'équation ac = b2 en un axiome d'existence, postulant que tout carré d'un nombre n (le terme médian "b"), tel que n > 1, peut s'exprimer comme le produit de deux nombres, l'un inférieur, l'autre supérieur à n (les termes extrêmes a et c).
La médiété peut, de cette manière, être lue comme une conjecture ou un théorème mathématique qui serait le suivant :
Pour tout b > 1, il existe une paire (a, c) telle que a < b < c, et telle que ac = b2. La preuve de ce théorème est du reste aisée à produire, puisqu'on peut montrer que pour tout nombre b supérieur à un, il existe au moins un couple de ce genre, qui est le couple (1, b2), où l'on a bien a < b < c. La formule ac = b2 prend simplement, dans cette formulation, la place de la formule "constructive", dont notre médiété dérive par extension.
A ces quelques remarques, on peut ajouter que les concepts de "double" et de "triple", qui découlent des premières applications de cette médiété, ont fait l'objet, dans l'antiquité, d'amples spéculations géométriques, comme dans le fameux problème de la duplication du cube, ce qui peut expliquer son appellation traditionnelle de médiété géométrique.
La médiété harmonique
Archytas :
"On parle de moyenne subcontraire, celle que nous appelons harmonique, quand le rapport de trois termes est le suivant : le premier terme dépasse le deuxième d'une fraction de lui-même et le moyen dépasse le troisième de la même fraction du troisième. "
Cette médiété se note :
b - a = a
c - b c
et ses plus petites valeurs possibles pour (a, b, c) sont (2, 3, 6).
D’autres auteurs anciens, tels que Platon ou Nicomaque, ont également défini cette médiété, et ont fait remarquer, comme Archytas, que la médiété harmonique entretient une relation directe avec la médiété arithmétique, puisqu’elle n’est autre qu’une moyenne arithmétique entre inverses.
En effet, il est assez simple de démontrer mathématiquement que des termes (a, b et c) sont en moyenne harmonique si et seulement si leurs inverses sont en moyenne arithmétique.
Cette remarque doit maintenant nous faire entrer dans des remarques structurelles.
Structure des médiétés 1, 2, 3
La médiété harmonique découle de l'arithmétique en prenant les inverses des termes de celle-ci, par quoi on la désigne du nom de sous-contraire ou subcontraire.
Ici se place un petit problème de vocabulaire. L'expression "sous-contraire", qui désigne la relation entre une fraction et son inverse, va devenir, après Archytas, une sorte de mot-valise, exprimant l'idée qu'à partir de la médiété Nicomaque 1, on peut retrouver toutes les autres, à ceci près que la relation d'inversion n'est pas appliquée aux mêmes endroits de la médiété. Selon les auteurs, l'expression "sous-contraire" désigne une formule pouvant être obtenue à partir d’une autre, soit en prenant les inverses de ses termes, soit en prenant les inverses de l'une ou l'autre des fractions qu'elle contient. La signification du terme "sous-contraire" s'élargit même en deux temps, de sorte qu'après avoir désigné, à partir d'Archytas, la relation de la médiété 3 à la médiété 1, il désignera, chez Théon de Smyrne, la relation du sous-ensemble des médiétés 4 à 6 à celle du sous-ensemble 1 à 3, et enfin la relation du sous-ensemble 7 à 12 au sous-ensemble 1 à 6. A y regarder de près, ces emplois du terme sous-contraire ne sont pas incompatibles, puisqu'ils délimitent des parties distinctes, mais complémentaires du système des médiétés.
Parallèlement à cette liaison entre les médiétés 1 et 3, on trouve chez de nombreux auteurs l'idée que les médiétés 1, 2 et 3 constituent une structure indépendante.
Commençons par nous faire une idée de la nature de cette "triangularité" qui est réalisée dans le sous-système des médiétés 1 à 3, formant le noyau logique du système général. Les trois médiétés sont identiques dans leur partie majeure, et ne se distinguent que par leur partie mineure. Le système de leurs différences doit donc trouver son expression dans le système de variation de la fraction mineure. Pour le saisir, il nous faut faire subir à cette fraction une rotation de 90 degrés, pour l'amener à représenter ce qu'elle est effectivement : un intervalle sur la chaîne, conventionnellement horizontale, des entiers. De cette manière, on s'aperçoit que, dans la médiété Nicomaque 1, cet intervalle est le minimum, puisqu'il est nul :
a / a (intervalle de rang zéro)
Tandis que, dans la médiété Nicomaque 3, cet intervalle est l'intervalle maximum, puisqu'il est l'intervalle entre les deux extrêmes:
a / c (intervalle de rang 2)
L'observation de ces deux formules permet donc de trouver déductivement la troisième, qui n'est autre que la formule intermédiaire entre les deux autres, où de ce fait l'intervalle est "moyen".
a/b (mais aussi b/c) (intervalles de rang 1)
Nous disons l'intervalle, mais il s'agit bien dans cette médiété Nicomaque 2 de deux intervalles a/b et b/c; de sorte qu'au triangle formé par la croissance de l'intervalle de la fraction mineure de la médiété

A cette structure donc s'oppose une structure en triangle qui est l'inverse de celle-là, et qui est celle du "nombre de fractions dans la partie mineure".
Médiété 1 : 3 fractions (a/a b/b c/c)
Médiété 2 : 2 fractions (a/b b/c)
Médiété 3 : 1 fraction (a/c) Décroissance du nombre de fractions
Une réflexion un peu attentive fera comprendre que cette seconde structure est un corrélat de la première, de sorte qu'on a affaire à deux structures triangulaires qui sont réciproques et duales l'une de l'autre.
Concernant cette double propriété de la triade des médiétés Nicomaque 1 à 3, de constituer à la fois le noyau et la matrice de toutes les suivantes, en même temps qu'un système achevé et clos sur lui-même, nous devons nous rappeler que ces trois médiétés sont celles qui se déduisent des rapports arithmétiques de la "grande tétractys" (6 - 8 - 9 - 12).
Comme l'a montré Nicomaque, alors que les termes 6, 9, 12 sont en proportion arithmétique, les termes 6, 8, 12, sont eux, en proportion harmonique.

Quant à la médiété géométrique, elle s'obtient, elle, par alternation des rapports 6 - 9 et 8 - 12.

Articulation de l'ensemble des médiétés 1 à 3 à celui des médiétés 4 à 6
A présent, le système triangulaire dont nous venons d'exposer les caractères de complétude et de clôture, ce système se définit aussi comme un sous-ensemble, au sein d'un ensemble de rang supérieur, comprenant, celui-là : "toutes les formules qui ont pour majeure la sous-formule (b - a) / (c - a)".
Cette définition du sous-ensemble des médiétés 1 à 6, notons le, nous renvoie déjà à la question de la clôture du système des médiétés, puisque nous verrons que le sous-ensemble des 6 médiétés restantes (de 7 à 12), pourra lui-même être défini comme l'ensemble des médiétés qui n'ont pas pour majeure la formule (b - a) / (c - a).
On voit que, dans cette situation gnoséologique particulière, l'hyper-ensemble, le système complet, est construit déductivement à partir de l'ensemble-noyau, par la simple considération de ce qui lui manque. Le système qui nous occupe à présent comprend 6 éléments, et la déduction des trois premières médiétés aux trois suivantes se fait, comme de coutume, par la mise en oeuvre d'un opérateur de "sous-contrariété".
En effet, les médiétés 4 à 6 sont des sous-contraires, de médiétés (ou plus exactement, comme on va le voir, de formules de médiétés) appartenant au groupe 1 à 3. Le "triangle" des médiétés (1-2-3) se voit doté d'un complément triangulaire, dont les éléments se déduisent des éléments du premier groupe en inversant les deux termes de la fraction mineure.
Mais que devons-nous remarquer tout de suite?
Que cette relation, la sous-contrariété, n'est pas biunivoque, mais comporte une dissymétrie. En effet :
a) La médiété 1 n'a pas de sous-contraire, puisqu'en inversant les termes de la fraction a/a on n'obtient pas une nouvelle formule, mais la même formule.
b) La médiété 2 possède deux sous-contraires, qui ne sont pas des propriétés distinctes d'une même médiété, mais bel et bien deux médiétés distinctes, dont les solutions sont différentes.
c) La médiété 3 ne possède qu'une sous-contraire.
Nous sommes à présent en mesure de reporter tout ceci sur un schéma topologique continu, dans lequel le triangle intérieur des médiétés (1-2-3) est la matrice du triangle des médiétés (4-5-6).
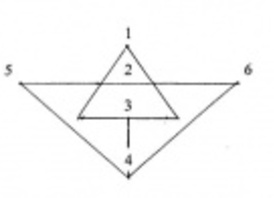
Remarquons toutefois que, pour exprimer cette relation topologique, on doit consentir à ce que la représentation de la médiété ne soit pas la même, dans le triangle (1-2-3) et dans le triangle (4-5-6). En effet, dans le triangle intérieur, une médiété est représentée par un segment (de longueur nulle pour la médiété 1), tandis que, dans le triangle extérieur, une médiété est représentée par un point topologique
Avant d'aborder, dans le prochain article, la partie démonstrative de cet exposé, faisons le point sur la question du développement historique de la théorie des médiétés. L'analyse structurale que nous venons de mener sur les médiétés 1 à 6 constitue un socle ancien et stable, que l’on trouve autant en accord avec Théon qu'avec Nicomaque. Mais à partir de là, tout change. Théon nous annonce 12 médiétés, les 6 dernières devant être une fois de plus les "sous-contraires" des 6 premières; mais, hélas, il ne nous détaille réellement que les médiétés 1 à 3. Nicomaque nous présente une "décade de médiétés", ce qui a très tôt éveillé un soupçon qui s'exprime ainsi : que vient faire ici la décade?
C'est à la question de la complétude du système des médiétés et à la détermination rigoureuse de leur nombre que sera consacré le prochain article.