La tétractys contient l'espace

 

 

 

LA TETRACTYS CONTIENT L’ESPACE

 

 

  

Les dimensions de l’espace

 

A chacun des quatre étages de la tétractys, correspondants aux nombres entiers, sont associées les 4 dimensions pythagoriciennes de l’espace que sont :

 

 1. Dimension du point.

 2. Dimension de la droite  (dim 1).

 3. Dimension du plan (dim 2) .

 4. Dimension du volume, ou de l'espace "euclidien" (dim 3) .

  

L’espace pythagoricien compte donc une dimension de plus que le nôtre, la dimension du point étant distinguée de celle de la droite, ce qui est une définition plus analytique que celle dont nous faisons usage, puisqu’à chaque étage de la tétractys correspond le nombre de points qui sont mathématiquement nécessaires pour déployer, ou paramétrer, chacune des dimensions considérées. En effet, il faut deux points pour paramétrer une droite, trois pour un plan, et quatre pour un volume.

Pour éviter les confusions, à partir d’ici on parlera uniquement en dimensions pythagoriciennes.

 

 

 

 Les objets premiers de la géométrie

 

De même que l’arithmétique pythagoricienne confère un statut distinctif aux quatre premiers nombres entiers, qui les distingue de l’infinité des suivants, la géométrie distingue quatre objets « premiers », qui sont les objets les plus simples que l’on puisse construire, dans chaque dimension, à partir d'éléments de dimensions inférieures.

 

En dimension 1, l’objet premier, et unique, n’est autre que le point lui-même.

En dimension 2, l’objet premier est le segment, dont la droite n’est autre que la dimension.

En dimension 3, l’objet premier est le triangle équilatéral, (dont la dimension est le plan) : figure qui a la propriété d’être le plus simple des polygones réguliers.

En dimension 4, l’objet premier est le tétraèdre (dont la dimension est le volume ou l’espace « euclidien ») : le plus simple des polyèdres réguliers.

  

                        

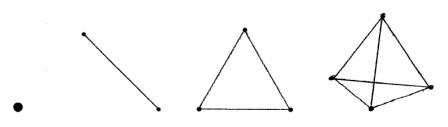
               Point            Segment          Triangle équilatéral         Tétraèdre

 

 

Là encore, la définition pythagoricienne est plus fine que celles qui nous sont habituelles, en ce qu'elle associe de façon rigoureuse, à chacun des objets géométriques élémentaires qui sont définis et délimités par des points (1, 2, 3 ou 4), le « fond » ou le réceptacle indéfini qui lui est propre, et qui n'est autre que sa dimension. Dimensions et objets premiers sont ainsi déployés au sein d'une relation générale, de laquelle chaque réalité reçoit son  juste statut. Ainsi, une droite ne peut jamais être considérée comme un objet défini, qui pourrait être représenté de quelque façon que ce soit, ou qui, a fortiori, pourrait "cohabiter", au sein d'une construction, avec des objets tels qu'un cercle ou un segment, puisqu'elle est une réalité indéfinie, analogue au plan ou à l’espace "euclidien". Pour la dimension 1, l’objet, qui est le point, est plus difficile à distinguer intuitivement de la dimension qui est la sienne; néanmoins les deux sont bien différents sur le plan logique, puisqu'un objet-point peut être défini, (par un couple de coordonnées, ou par sa relation avec un autre point), alors que sa dimension reste indéfinie.

Ainsi, dans le même espace où la géométrie euclidienne parvient à ne compter que trois "choses", trois dimensions, la géométrie pythagoricienne dénombre 8 réalités différentes, 4 définies et 4 indéfinies, recevant leur statut les unes des autres.

 

 

Un point délicat

 

Dans la construction des objets premiers de la géométrie, nous devons remarquer que la géométrie pythagoricienne ne met pas seulement en jeu les propriétés numériques de la tétractys, les nombres 1 à 4. Ce qui est en jeu est en réalité plus subtil, et concerne en outre le rapport arithmétique que chaque ligne de la tétractys entretient avec celle qui la précède dans le temps.

En effet, il faut 2 objets de la catégorie 1, à savoir deux points, pour construire un segment, (2x1 unités-points)

Il faut 3 objets de la catégorie 2, à savoir trois segments, pour construire un triangle équilatéral (3x2x1 unités-points).

Enfin, il faut 4 objets de la catégorie 3,  à savoir quatre triangles équilatéraux, pour construire un tétraèdre (4x3x2x1) unités-points. Autrement dit, dans le tétraèdre, la tétractys est reconstituée de façon régressive sous la forme d’un produit de nombres, qui récapitule l’ensemble des mouvements accomplis depuis le point originaire. 

Là encore, le niveau le plus abstrait est le niveau 1. En effet, la première ligne n’entretient pas de relation avec celle qui la précède, puisqu’aucune ne la précède, mais avec elle-même. De sorte qu’on doit réellement comprendre qu’il faut 1 objet de la catégorie 1 pour construire l'objet le plus simple de cette même catégorie 1 (1x1) unité-point.

  

  

 1 x 1             2 x 1                     3 x 2 x 1                     4 x 3 x 2 x 1

 

  

Dans cette application : aux quatre objets premiers de la géométrie sont donc associées, de façon biunivoque, les factorielles des quatre premiers nombres. 

Ces précisions nous permettent de définir avec plus de justesse le statut exact des objets premiers de la géométrie pythagoricienne. Au sens strictement mathématique, les objets premiers ne sont pas les objets les plus simples qui existent dans leur dimension respective. En dimension 3, le cercle est un objet plus simple que le triangle, premier des polygones, puisqu'on peut le définir avec 2 points seulement. Même chose pour la sphère, qui, en dimension 4, est un objet plus simple que le tétraèdre, puisqu'elle aussi ne nécessite que deux points pour être définie. En toute rigueur donc, les objets premiers doivent être définis comme les premiers objets que l'on puisse construire, dans chaque dimension,  avec le matériel le plus simple de la dimension inférieure.  La série des objets premiers est donc une méthode de construction dans laquelle on exige que l'objet le plus complexe se laisse entièrement décomposer en éléments discrets de dimensions inférieures, jusqu'à l'unité.

  

 

Récapitulons.

Le chemin parcouru jusqu’ici avait pour objet d’illustrer deux énoncés canoniques de la mathématique pythagoricienne  : « la tétractys contient le nombre »,  « la tétractys contient l’espace ».

Mais on a vu que la deuxième proposition devait se comprendre selon deux chemins, dont l’un est court, synthétique, et consiste à dire : « Il suffit de quatre pas, - quatre points - pour construire les dimensions de l’espace; tandis que l’autre est analytique, et consiste à détailler le rapport qu’entretient chaque ligne de la tétractys, soit avec elle-même (pour la première), soit avec celles qui la précèdent dans le temps, pour les trois suivantes.

La construction du tétraèdre, qui était le but de cet article, peut elle-même être comprise comme la synthèse de ces deux cheminements, l’un court, l’autre détaillé. En effet, il peut suffire de deux points pour définir un segment, trois pour un triangle, et 4 points pour définir un tétraèdre : ses 4 sommets, ou, indifféremment, les centres de ses quatre faces; et, si l'on choisit les sommets, cette construction peut s’effectuer par la simple projection d’un point d’un sommet à un autre. (On voit même que, dans ce cas, seuls trois "mouvements" sont en réalité nécessaires, correspondant au déploiement de nos dimensions "euclidiennes"; néanmoins, en pythagorisme, la « position » du point initial compte comme un mouvement à part entière.)

Mais il est également possible de construire le tétraèdre de la façon analytique indiquée plus haut, qui explicite cette fois, le rapport de chaque objet avec celui qui le précède dans le temps, et dans ce cas, ce sont 4 triangles, donc 12 segments, donc 24 points en tout qui seront nécessaires à sa construction.

On verra que ces précisions, bien que délicates, seront utiles pour aborder  le domaine qui se présente à nous maintenant, et qui est celui de la théorie musicale.