-
Gnomon d'un polyèdre régulier
GNOMON D’UN POLYEDRE REGULIER
Les polyèdres réguliers
On appelle ici polyèdres réguliers (ou solides réguliers), suivant l'usage commun, la seule famille étroite des polyèdres réguliers convexes, appelés aussi solides pythagoriciens, ou, abusivement, platoniciens. Les polyèdres réguliers convexes sont au nombre de 5, tandis qu'avec les concaves, la famille s'élargit à 9.
Les polyèdres réguliers sont à la famille des polyèdres, ce que les polygones réguliers sont à la famille des polygones. En pythagorisme, ils appartiennent à la catégorie des objets géométriques "premiers en naissance". De même que les polygones réguliers (dimension 3) sont construits avec le matériel le plus simple que l'on puisse trouver dans la dimension inférieure (des segments de longueur identique), de même, les polyèdres réguliers (dimension 4) sont construits avec les objets les plus simples de la dimension inférieure : des polygones réguliers identiques.
Tétraèdre Cube

Octaèdre Dodécaèdre Icosaèdre
Leurs faces sont toutes des polygones réguliers identiques, leurs angles et leurs sommets sont tous identiques. Mathématiquement, ils sont absolument symétriques en chacune de leurs faces, de leurs angles et de leurs sommets (symétrie de rotation).
Les propriétés principales de ces figures étant bien connues et documentées (les plus importantes étant, outre la démonstration qu'il n'en existe que cinq, la dualité et la loi d'Euler), on se dispensera de les rappeler ici, pour nous limiter à ce qui concerne la théorie du gnomon.
*
Si l’on applique aux polyèdres une méthode de construction analogue à celle employée pour les polygones, alors :
Seul le cube possède un gnomon tridimensionnel.
Dans un polygone gnomonique, triangle ou carré, on remarque cette propriété particulière que la graine (la forme géométrique à reconstituer, considérée comme l’origine de la série des gnomons) et l’atome (l’élément unique, ou « brique topologique » servant à la construction des gnomons) sont identiques.
Dans le cas des polyèdres réguliers, cette propriété (identité de la graine et de l’atome) est observée pour le cube, et pour le cube seulement.
Avec plusieurs petits cubes de même taille, on peut en effet construire un cube plus grand, mais la chose s’avère impossible pour chacun des 4 autres polyèdres réguliers. Avec plusieurs petits tétraèdres, il est impossible de construire un plus grand tétraèdre, idem pour l’octaèdre, le dodécaèdre et l’icosaèdre.
Le gnomon facial
Ce qui suit n’est donc plus un raisonnement portant sur la constitution interne de l’objet, mais uniquement sur sa structure et son aspect externe, autrement dit sur sa face.
On appelle maintenant gnomon facial d’un polyèdre, le solide qui, ajouté à ce polyèdre, permet de reconstituer un polyèdre semblable, dont la face est un polygone gnomonique de rang supérieur.
En suivant cette définition, 4 des 5 polyèdres réguliers possèdent un gnomon facial.
Simplement, dans 3 de ceux-ci, la graine (la forme à reproduire) n’est pas identique à l’atome (la brique de construction), et l’atome n’est pas unique (deux atomes pour le tétraèdre et l’octaèdre, trois atomes pour l’icosaèdre).
Complétude du système
Parmi les 5 polyèdres réguliers, l’un d’entre eux, le dodécaèdre, ne peut pas posséder de gnomon facial.
Démonstration.
La démonstration s’appuie sur celle que nous avons donnée plus haut, montrant que, parmi les polygones réguliers, seuls le triangle équilatéral et le carré possèdent un gnomon.
En effet, d’après cette limitation, pour qu’un polyèdre puisse avoir un gnomon facial, il faut de toute nécessité que sa face soit ou bien un triangle, ou bien un carré. La face du dodécaèdre étant un pentagone, celui-ci ne peut avoir de gnomon facial, puisque le pentagone n’est pas une solution de pavage continu du plan.
Quant aux quatre autres polyèdres réguliers, nous allons voir que chacun d’eux possède effectivement un gnomon facial.
A la fin de cet article, un tableau récapitule les valeurs des 4 premiers gnomons de ces polyèdres.
Gnomon du cube
Le cube est, comme on l’a vu, le seul polyèdre régulier dont le gnomon n’est pas seulement un gnomon facial, mais un gnomon au sens interne et constitutif du terme, puisque, dans celui-ci, la graine, la forme à reproduire, est identique à l’atome, pièce unique servant à sa construction.
Les premiers gnomons du cube correspondent aux nombres : 7, 19, 37, 61, etc,
et la règle qui permet de les trouver est la suivante :
G (c) = 1 (+ 6), (+12), (+18), (+24), (...), (+ 6 x n)
Mais pour comprendre cette série, il est encore plus simple de considérer les nombres correspondants à chacun des cubes gnomoniques reconstitués. En effet, ces nombres sont tout simplement les cubes des nombres entiers naturels.
1, 8, 27, 64, 125, ..., n3
Nous voyons ainsi que la théorie « classique » des nombres cubiques, telle qu’elle est passée sans altération de la tradition pythagoricienne jusqu'à nous, est elle aussi en accord avec la définition mathématique rigoureuse du gnomon, contrairement à la théorie malencontreuse des nombres « figurés », qui en est une tentative d'extension illégitime. Dans cette théorie classique, les nombres appelés cubiques sont les nombres correspondants à chacun des cubes gnomoniques reconstitués, chacune des phases de « réalisation » ou de complétude du cube, incluant la graine, l’unité, dans la série. Si nous avons adopté la convention de nommer « cube » la puissance 3 d’un nombre, de la même manière qu’on appelle « carrés » les nombres correspondants à la croissance de la surface du carré gnomonique, c’est donc là aussi par référence à une théorie mathématique exacte du gnomon.
Le fameux « Rubix-Cube » peut être pris comme un exemple valable de cube gnomonique (gnomon d'ordre 2). S’il était réellement constitué uniquement de petits cubes, il serait constitué de 27 éléments : 33.

Gnomon du tétraèdre
Pour chacun de nos gnomons futurs, la graine est coloriée en rouge, l’atome-octaèdre en blanc et l’atome-tétraèdre en gris.


Tétraèdre Gnomon du tétraèdre
On peut vérifier visuellement que la face du grand tétraèdre (triangle gnomonique de rang 2) est bien un gnomon polygonal de celle du petit tétraèdre – en rouge – qui est sa graine.
Le gnomon (facial) du tétraèdre est un solide en forme de pyramide (tétraédrique) tronquée, composé de 4 éléments : 1 octaèdre et 3 tétraèdres. La série infinie des gnomons suivants se développe ainsi :
G (t) = (1/3); (3/6); (6/10); (10/15); (15/21); (21/28); ...; (a/b)
On appelle « b » la valeur de droite de chaque fraction, correspondant aux atomes-tétraèdres. On voit que les valeurs successives de b sont engendrés à partir de la première (3), par les opérations :
b = 3; +3; +4; +5; +6; …
Notons que la graine du gnomon peut être intégrée dans la série des « b » sans déroger à la règle + n (avec n supérieur à 1) qui est celle de la série, puisqu’on a :
1 (graine) + 2 (premier gnomon), +3, +4, etc
Quant à la valeur « a », valeur de gauche de chaque fraction, correspondant aux atomes-octaèdres, elle n’est autre, à chaque fois, que la valeur « b » de la fraction précédente (y compris la première « 1 » qui correspond à la valeur b du rang précédent, qui est le rang de la graine). La série des valeurs « a » est identique à la série des « b », mais avec un temps de retard.
A présent, il est particulièrement intéressant d’opérer la simplification de ces fractions.
On observe ceci :
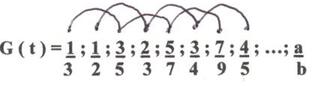
En suivant le développement de la valeur "a" selon deux chaînes alternées, on s’aperçoit que ces deux chaînes nous présentent, l’une, la série des nombres impairs et, l’autre, la série des nombres entiers.
a = 1, …, 3, …, 5, …, (série des nombres impairs)
a =…, 1, …, 2, …, 3, … (série des nombres entiers)
Le constat est le même pour la valeur b, mais avec un rang de décalage :
b = 3, …, 5, …, 7, … (série des nombres impairs supérieurs à 1)
b =…, 2, …, 3, …, 4, … (série des nombres entiers supérieurs à 1)
En résumé, dans cette alternance de fractions, la première chaîne :
G (t) = (1/3); (...); (3/5); (...); (5/7): ...
exprime le rapport de chaque nombre impair à son successeur.
La deuxième chaîne :
G (t) = (...); (1/2); (...); (2/3); (...); (3/4); ...
exprime le rapport de chaque nombre entier à son successeur.
Gnomon de l’octaèdre
Le gnomon de l’octaèdre est constitué des mêmes éléments atomiques que celui du tétraèdre : tétraèdres et octaèdres. Seule leur proportion change donc.


Octaèdre Gnomon de l’octaèdre
La face du grand octaèdre est bien un gnomon polygonal de celle du petit octaèdre (graine).
Le gnomon immédiat de l’octaèdre est constitué de 5 octaèdres et 8 tétraèdres.
Les gnomons ultérieurs se développent de la façon suivante :
G (o) = (5/8); (13/16); (25/28); (41/44); (61/64); ...; (a/b)
On remarque que la valeur de a évolue selon la règle suivante :
a = 5 ; +8 ; +12 ; +16 ; +20 ; …
Notons que, là aussi, la graine du gnomon, constituée d’1 octaèdre, peut être comprise dans la série des valeurs « a » à titre de terme originaire, sans faire exception à la règle (+ 4 x n) qui régit la suite des gnomons.
En effet :
1 (graine) +4 = ; 5 (premier gnomon); +8; +12; …
Quant à la valeur b, on remarque qu’elle se déduit directement de a, puisque l’on a :
b = a + 3
Gnomon de l’icosaèdre
Le gnomon de l’icosaèdre se construit au moyen des deux mêmes éléments atomiques que les gnomons du tétraèdre et de l’octaèdre : des octaèdres (a) et des tétraèdres (b); cependant le système inclue un élément atomique de plus (d) qui est la propre graine de l’icosaèdre.
Les valeurs de ce gnomon évoluent beaucoup plus rapidement que celles des précédents, puisque le premier gnomon de l’icosaèdre est déjà composé de 20 octaèdres et 60 tétraèdres.
Voici la façon dont ce solide se construit.
Sur chacune des 20 faces de l’icosaèdre (en rouge), on « colle » un octaèdre. La figure qui apparaît ensuite est celle d’un ballon sur lequel 12 cratères ou cupules se présentent, correspondants aux 12 sommets de l’icosaèdre primitif. Dans chacune de ces 12 cupules se logent 5 tétraèdres, soit 12 x 5 = 60 tétraèdres en tout.
Comme il était fastidieux de réaliser en papier les 81 solides nécessaires à cette construction, on n’en a réalisé ici qu’une partie, suffisante pour en détailler les trois étapes.
Gnomon de l’icosaèdre (construction) Cupule remplie de 5 tétraèdres (en haut)
et face complète du grand icosaèdre (en bas)
En dépit de ses dimensions imposantes, ce gnomon est bien un gnomon facial du premier rang, (dont la face est un triangle gnomonique de rang 2); de sorte que le rapport 20/60 est l’équivalent exact, pour l’icosaèdre, des rapports 1/3 et 5/8 enregistrés pour les polyèdres précédents.
Quant au calcul des valeurs suivantes de l’icosaèdre, il ne pose guère de difficulté, puisqu’on remarque immédiatement que ces valeurs sont égales à 20 fois celles du tétraèdre. Déroulons l’une au dessus de l’autre les deux séries de gnomons :
G (t) = (1/3); (3/6); (6/10); (10/15); (15/21); ...; (a/b)
G (i) = (20/60); (60/120); (120/200); (200/300); (300/420); ...; (a/b)
Les valeurs du gnomon de l’icosaèdre (en bas) se déduisent de celles du tétraèdre (en haut), en multipliant celles-ci par 20.
Autrement dit, on a :
G ( i ) = G ( t ) x 20
Tableau récapitulatif des valeurs des 4 premiers gnomons des polyèdres réguliers
Le tableau qui suit indique, pour chacun des polyèdres gnomoniques, les valeurs de ses quatre premiers gnomons.
graine
Gnomon 1
Gnomon 2
Gnomon 3
Gnomon 4
cube
1c
7c
19c
37c
61c
Total PG
1c
8c
27c
64c
125c
tétraèdre
1b
1a, 3b
3a, 6b
6a, 10b
10a, 15b
Total PG
1b
1a, 4b
4a, 10b
10a, 20b
20a, 35b
octaèdre
1a
5a, 8b
13a, 16b
25a, 28b
41a, 44b
Total PG
1a
6a, 8b
19a, 24b
44a, 52b
85a, 96b
icosaèdre
1d
20a, 60b
60a, 120b
120a, 200b
200a, 300b
Total PG
1d
1d, 20a, 60b
1d, 80a, 180b
1d,200a, 380b
1d,400a, 680b
a : octaèdre
b : tétraèdre
c : cube
d : icosaèdre
PG : polyèdre gnomonique