-
La mathématique pythagoricienne
par Guillaume DENOM
Apprendre à compter jusqu'à quatre, mais sans rien oublier en chemin, et en étant attentif à remarquer, chaque fois, ce qui est clos et complet au nombre quatre : tel est le programme mathématique proposé par Pythagore.
Une figure, un pas.
« Symboles pythagoriciens », Protreptique, Jamblique
Par celui qui transmit à notre âme la tétractys sacrée, source de la Nature dont le cours est éternel.
Serment pythagoricien, Vers d’or de Pythagore
La décade est également appelée Foi. L’explication donnée par Philolaos est que, lorsque nous cherchons à saisir la réalité de manière approfondie, nous accordons à la décade et à ses parties une foi inébranlable.
Théologoumènes arithmétiques, Pseudo-Jamblique
C’est le Nombre qui, en rendant toutes choses adéquates à l’âme par la sensation, les rend connaissables et commensurables entre elles selon la nature du gnomon.
Fragments, Philolaos
* * *
Si, pour le grand public, l’héritage mathématique de Pythagore est associé au théorème de l’hypoténuse qui a emprunté son nom, bien qu’il ait été connu longtemps avant Pythagore, pour les pythagoriciens, cet héritage consiste, principalement, en quatre notions mathématiques, notions qui ne sont pas seulement des théories, mais des idées mathématiques au sens le plus fort, incluant chacune une variété indéfinie de théories. Ces notions fondamentales sont : la tétractys, les médiétés, le gnomon et les solides réguliers.
Parmi ces quatre notions, la première, la tétractys, a en outre la propriété de contenir les trois qui la suivent. C’est à relier ces notions par le chemin mathématique le plus court que sera consacré cet exposé.
La mathématique pythagoricienne est une mathématique élémentaire, dans les deux sens que revêt ce mot. D’une part, elle ne comporte rien de très difficile, rien qui soit hors d’atteinte d’un lecteur cultivé; - et, pour ce qui concerne le présent exposé, ceux qui seraient rebutés par les démonstrations pourront, sans inconvénient pour la suite, laisser de côté les articles 6 et 7 de la première section, où se trouve concentrée la seule partie démonstrative de ce texte. Mais d’autre part, la mathématique pythagoricienne est élémentaire en ce qu’elle porte sur les principes, les éléments premiers de la mathématique, qu’elle se propose de définir et de fonder à partir d’une seule pensée originaire.
Cette mathématique est donc une réflexion sur le concept général de la science, qui s’attache à définir ce qui est premier dans chacun des domaines où celle-ci peut s’exercer. Par ce côté, son propos aura peut être plus de chance d’intéresser le philosophe ou l’épistémologue, que le mathématicien spécialisé, installé dans ses habitudes modernes.
Il ne sera presque jamais question, ici, des débats contemporains relatifs à l’histoire du pythagorisme. En l’absence de tout document sur le savoir de Pythagore, les historiens se trouvent réduits à des suppositions purement conjecturales. De plus, la plupart sont dominés, voire possédés, par le préjugé moderne que la science a toujours évolué par une progression graduée. Le plus ancien traité de mathématique connu étant les Eléments d’Euclide, ils sont conduits à supposer toute une série de « progrès » de Pythagore à Platon, à Aristote ou à Euclide ; alors même que ce qui s’est produit durant cette période est exactement le contraire, savoir, une série de régressions sans équivalent dans l’histoire de la pensée, véritables catastrophes intellectuelles qui ont abouti à ce que la science, dont les principes s'étaient dévoilés dans toute leur pureté dans la pensée d’un homme, s’est retrouvé enfouie et emprisonnée pendant deux millénaires.
Abandon de la doctrine du nombre naturel au profit du nombre « idéal » (Platon) ; abandon de la logique mathématique au profit de la logique langagière, abandon de la physique mathématique au profit d’une physique purement empirique, abandon de la cosmologie héliocentrique au profit du géocentrisme (Aristote) ; enfin, abandon de la primauté du nombre sur la figure (Euclide) : tels sont les principaux « progrès » survenus entre l’époque de Pythagore et celle qu’on a coutume de considérer comme l’âge d’or de la pensée grecque.
A la fin du XIXe siècle, certains historiens ont cru reconnaître dans la mathématique pythagoricienne des conceptions ressemblantes à celles de la mathématique moderne; et ils ont forgé l’expression d’ « algèbre géométrique » pour caractériser cet ensemble de spéculations, situées à l'interface entre la théorie du nombre et la géométrie, sans s’apercevoir que le domaine défini par ces spéculations était celui de la logique mathématique, dont l’objet est de traiter, précisément, des structures communes à ces deux sciences : arithmétique et géométrie.
Alors, plutôt que d’entrer dans les vues de ces historiens autoproclamés, qui ne sont en réalité que de modernes mythographes, et qui, à force d’enfermement dans la méthode critique, de refus de la tradition pythagoricienne, ont tendu de plus en plus à déposséder Pythagore de toute pensée originale, on se fiera plutôt au sentiment de ceux qui furent les restaurateurs de la science, les Copernic, Kepler, Newton, tous pythagoriciens fervents*, et qui étaient pleinement conscients de renouer avec ce fil ancien de la pensée.
*Avec son mépris ou son indifférence pour les "mathématiques pures" (autres qu'appliquées aux problèmes physiques), et sa robuste philosophie de marchand de lunettes, l'anti-pythagoricien Galilée demeure, il est vrai, le père de la science "positive" et technicienne; cette science qui a libéré l'homme du souci de la connaissance absolue, en acceptant de limiter son intelligence à la seule distinction de "ce qui marche" et "ce qui ne marche pas".
-
DE LA TETRACTYS AUX MEDIETES
LA TETRACTYS CONTIENT LE NOMBRE
La théorie du Nombre
A la question : « qu’est-ce qui est premier en mathématique? » la mathématique pythagoricienne répond sans hésiter : ce qui est premier est le Nombre.
Bien qu’elle puisse paraître anodine, cette particularité distingue radicalement la mathématique pythagoricienne de toute autre mathématique existante. Chez Euclide, l’arithmétique, science du nombre, se présente comme une division, ou une spécialisation, de la géométrie. Les nombres sont représentés par des segments de droites. Dans la mathématique moderne, la théorie du nombre est fréquemment subordonnée à une notion logique, telle que la notion d’ensemble, ou à une quelconque théorie axiomatique.
Bien que le nombre soit « premier en naissance », le but de la mathématique pythagoricienne est de construire, ou de produire, dans une seule et même pensée originaire, ces trois parties de la mathématique que sont : l’arithmétique, la géométrie et la logique, la troisième étant définie comme l’interface ou la « paroi » entre les deux premières. La tétractys est un concept mathématique qui présente ces trois aspects, et les présente sur un mode très particulier qui est celui de la synthèse, au sens même où Kant qualifie les jugements mathématiques de «synthétiques a priori ».
Le Quatre-Réceptacle
Le Quatre-Réceptacle est une étymologie possible du mot « tétractys », selon une tradition.* Si cette étymologie est incertaine, le sens mathématique de l'expression "tétractys", lui, est garanti par la multitude, autant que par la constance de ses applications, et on peut le traduire par l'expression française "clôture à quatre", ou "clôture quaternaire".
De même que le Nombre est « premier en naissance », et la science du nombre première par rapport aux deux autres parties de la mathématique (géométrie, logique), la mathématique pythagoricienne considère, au sein de l’infinité des nombres, certains nombres comme « premiers en naissance » relativement à tous les autres; et, pour des raisons très précises, elle décide de limiter ces nombres-principes à quatre : les quatre premiers nombres entiers.
Cet acte de clôture est un acte analogue, et mathématiquement équivalent, au choix d’une base arithmétique, telle que notre base 10. La différence étant qu’ici, l’action de clôture s’effectue non seulement dans l’ordre des nombres, mais simultanément dans trois ordres mathématiques différents : arithmétique, géométrique et logique.
La Tétractys
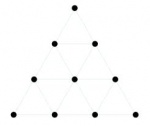
La tétractys est une notion mathématique qui associe la croissance du nombre entier naturel, à la croissance d’une figure géométrique : le triangle équilatéral.
La tétractys est « une certaine façon de compter jusqu’à quatre », dans laquelle les nombres sont représentés par des points.
L'unité, objet élémentaire de l'arithmétique, est coordonnée au point, objet élémentaire de la géométrie.
Il existe de nombreuses définitions mathématiques de la tétractys. Par exemple :
La tétractys est une constellation de dix points équidistants du plan, distribués en symétrie hexagonale, et formant un triangle équilatéral.
Ou encore cette définition qui ne fait appel qu'à des figures géométriques simples :
La tétractys est une constellation de points dont les positions sont définies par les sommets d'un hexagone et d’un trépied, inscrits ensemble dans un même triangle équilatéral.

« Réceptacle de l’illimité »
« La tétrade contient la décade. » En vertu de l’égalité : 1+2+3+4 = 10, la clôture du compte jusqu’à 4 coïncide avec la clôture, habituelle pour nous, de la base 10. Chez les anciens, le terme Décade est fréquemment employé comme synonyme de la tétractys
Mais, dans la tradition pythagoricienne, la tétractys est appelée « réceptacle de l’illimité », ce qui signifie que les quatre premiers nombres contiennent en puissance tous les autres.
Cette assertion peut être comprise selon une interprétation « naïve ». La tétractys étant une structure qui associe la croissance du nombre entier à la croissance du triangle, le même procédé peut être répété à l’infini, par l’ajout de nouvelles lignes sous la base du triangle.
Mais ce serait oublier que la tétractys est une structure « close ». En arithmétique, la clôture de la base implique toujours que : « on arrête, puis on recommence », comme c’est le cas dans le système décimal où, parvenu à 10, on reprend le compte à partir du début : 11, 12, 13...
Après avoir construit la première tétractys, on doit donc construire deux tétractys en même temps, celle de la seconde dizaine, et celle de la centaine, en application cette fois de l’égalité : 10+20+30+40=100. A partir de 101, ce sont trois tétractys qui se construisent en même temps; et notre tétractys se développe comme une figure « fractale » qui envahit l’espace à partir du sommet dont elle est issue.
100

200 300
Nombres décimaux et négatifs
Mais la correspondance entre le nombre et la figure peut évidemment être poussée plus loin, sans que soit trahi en rien l’esprit de la notion pythagoricienne.
En effet, rien n’interdit de considérer chacun des dix points de la tétractys comme étant lui-même un triangle, indéfiniment décomposable en parties tétractyques décimales de rangs inférieurs (tétractys à points triangulaires). De cette manière, la tétractys s’avère capable d’exprimer tous les nombres décimaux.
Entier « 1 » (origine)

Valeurs décimales, centésimales, etc.
Pour les nombres négatifs, il suffit d’opposer à la tétractys une anti-tétractys, selon le schéma suivant.
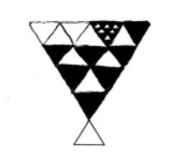
Pour le nombre zéro lui-même, il suffit d’indiquer que la tétractys et l’anti-tétractys sont, l’une et l’autre, vides.

En langage moderne, on dira que, pour peu qu'une règle de construction soit précisée, telle que "de haut en bas et de gauche à droite", la tétractys à points triangulaires contient un système de coordonnées biunivoque de l'ensemble des nombres entiers, mais aussi des nombres décimaux et négatifs.
*Le sens le plus généralement admis étant celui de "quadruple rayon" ou "rayonnement quadruple."
-
LA TETRACTYS CONTIENT L’ESPACE
Les dimensions de l’espace
A chacun des quatre étages de la tétractys, correspondants aux nombres entiers, sont associées les 4 dimensions pythagoriciennes de l’espace que sont :
1. Dimension du point.
2. Dimension de la droite (dim 1).
3. Dimension du plan (dim 2) .
4. Dimension du volume, ou de l'espace "euclidien" (dim 3) .
L’espace pythagoricien compte donc une dimension de plus que le nôtre, la dimension du point étant distinguée de celle de la droite, ce qui est une définition plus analytique que celle dont nous faisons usage, puisqu’à chaque étage de la tétractys correspond le nombre de points qui sont mathématiquement nécessaires pour déployer, ou paramétrer, chacune des dimensions considérées. En effet, il faut deux points pour paramétrer une droite, trois pour un plan, et quatre pour un volume.
Pour éviter les confusions, à partir d’ici on parlera uniquement en dimensions pythagoriciennes.
Les objets premiers de la géométrie
De même que l’arithmétique pythagoricienne confère un statut distinctif aux quatre premiers nombres entiers, qui les distingue de l’infinité des suivants, la géométrie distingue quatre objets « premiers », qui sont les objets les plus simples que l’on puisse construire, dans chaque dimension, à partir d'éléments de dimensions inférieures.
En dimension 1, l’objet premier, et unique, n’est autre que le point lui-même.
En dimension 2, l’objet premier est le segment, dont la droite n’est autre que la dimension.
En dimension 3, l’objet premier est le triangle équilatéral, (dont la dimension est le plan) : figure qui a la propriété d’être le plus simple des polygones réguliers.
En dimension 4, l’objet premier est le tétraèdre (dont la dimension est le volume ou l’espace « euclidien ») : le plus simple des polyèdres réguliers.
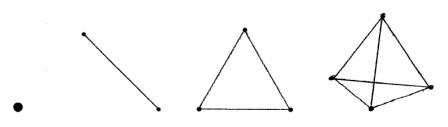
Point Segment Triangle équilatéral Tétraèdre
Là encore, la définition pythagoricienne est plus fine que celles qui nous sont habituelles, en ce qu'elle associe de façon rigoureuse, à chacun des objets géométriques élémentaires qui sont définis et délimités par des points (1, 2, 3 ou 4), le « fond » ou le réceptacle indéfini qui lui est propre, et qui n'est autre que sa dimension. Dimensions et objets premiers sont ainsi déployés au sein d'une relation générale, de laquelle chaque réalité reçoit son juste statut. Ainsi, une droite ne peut jamais être considérée comme un objet défini, qui pourrait être représenté de quelque façon que ce soit, ou qui, a fortiori, pourrait "cohabiter", au sein d'une construction, avec des objets tels qu'un cercle ou un segment, puisqu'elle est une réalité indéfinie, analogue au plan ou à l’espace "euclidien". Pour la dimension 1, l’objet, qui est le point, est plus difficile à distinguer intuitivement de la dimension qui est la sienne; néanmoins les deux sont bien différents sur le plan logique, puisqu'un objet-point peut être défini, (par un couple de coordonnées, ou par sa relation avec un autre point), alors que sa dimension reste indéfinie.
Ainsi, dans le même espace où la géométrie euclidienne parvient à ne compter que trois "choses", trois dimensions, la géométrie pythagoricienne dénombre 8 réalités différentes, 4 définies et 4 indéfinies, recevant leur statut les unes des autres.
Un point délicat
Dans la construction des objets premiers de la géométrie, nous devons remarquer que la géométrie pythagoricienne ne met pas seulement en jeu les propriétés numériques de la tétractys, les nombres 1 à 4. Ce qui est en jeu est en réalité plus subtil, et concerne en outre le rapport arithmétique que chaque ligne de la tétractys entretient avec celle qui la précède dans le temps.
En effet, il faut 2 objets de la catégorie 1, à savoir deux points, pour construire un segment, (2x1 unités-points)
Il faut 3 objets de la catégorie 2, à savoir trois segments, pour construire un triangle équilatéral (3x2x1 unités-points).
Enfin, il faut 4 objets de la catégorie 3, à savoir quatre triangles équilatéraux, pour construire un tétraèdre (4x3x2x1) unités-points. Autrement dit, dans le tétraèdre, la tétractys est reconstituée de façon régressive sous la forme d’un produit de nombres, qui récapitule l’ensemble des mouvements accomplis depuis le point originaire.
Là encore, le niveau le plus abstrait est le niveau 1. En effet, la première ligne n’entretient pas de relation avec celle qui la précède, puisqu’aucune ne la précède, mais avec elle-même. De sorte qu’on doit réellement comprendre qu’il faut 1 objet de la catégorie 1 pour construire l'objet le plus simple de cette même catégorie 1 (1x1) unité-point.

1 x 1 2 x 1 3 x 2 x 1 4 x 3 x 2 x 1
Dans cette application : aux quatre objets premiers de la géométrie sont donc associées, de façon biunivoque, les factorielles des quatre premiers nombres.
Ces précisions nous permettent de définir avec plus de justesse le statut exact des objets premiers de la géométrie pythagoricienne. Au sens strictement mathématique, les objets premiers ne sont pas les objets les plus simples qui existent dans leur dimension respective. En dimension 3, le cercle est un objet plus simple que le triangle, premier des polygones, puisqu'on peut le définir avec 2 points seulement. Même chose pour la sphère, qui, en dimension 4, est un objet plus simple que le tétraèdre, puisqu'elle aussi ne nécessite que deux points pour être définie. En toute rigueur donc, les objets premiers doivent être définis comme les premiers objets que l'on puisse construire, dans chaque dimension, avec le matériel le plus simple de la dimension inférieure. La série des objets premiers est donc une méthode de construction dans laquelle on exige que l'objet le plus complexe se laisse entièrement décomposer en éléments discrets de dimensions inférieures, jusqu'à l'unité.
Récapitulons.
Le chemin parcouru jusqu’ici avait pour objet d’illustrer deux énoncés canoniques de la mathématique pythagoricienne : « la tétractys contient le nombre », « la tétractys contient l’espace ».
Mais on a vu que la deuxième proposition devait se comprendre selon deux chemins, dont l’un est court, synthétique, et consiste à dire : « Il suffit de quatre pas, - quatre points - pour construire les dimensions de l’espace; tandis que l’autre est analytique, et consiste à détailler le rapport qu’entretient chaque ligne de la tétractys, soit avec elle-même (pour la première), soit avec celles qui la précèdent dans le temps, pour les trois suivantes.
La construction du tétraèdre, qui était le but de cet article, peut elle-même être comprise comme la synthèse de ces deux cheminements, l’un court, l’autre détaillé. En effet, il peut suffire de deux points pour définir un segment, trois pour un triangle, et 4 points pour définir un tétraèdre : ses 4 sommets, ou, indifféremment, les centres de ses quatre faces; et, si l'on choisit les sommets, cette construction peut s’effectuer par la simple projection d’un point d’un sommet à un autre. (On voit même que, dans ce cas, seuls trois "mouvements" sont en réalité nécessaires, correspondant au déploiement de nos dimensions "euclidiennes"; néanmoins, en pythagorisme, la « position » du point initial compte comme un mouvement à part entière.)
Mais il est également possible de construire le tétraèdre de la façon analytique indiquée plus haut, qui explicite cette fois, le rapport de chaque objet avec celui qui le précède dans le temps, et dans ce cas, ce sont 4 triangles, donc 12 segments, donc 24 points en tout qui seront nécessaires à sa construction.
On verra que ces précisions, bien que délicates, seront utiles pour aborder le domaine qui se présente à nous maintenant, et qui est celui de la théorie musicale.
-
L’INVENTION DE LA THEORIE MUSICALE
Une tradition assez unanime attribue à Pythagore une invention capitale de l’histoire de la pensée, qui est la découverte des rapports mathématiques correspondants aux principaux accords musicaux. L’histoire nous en a été transmise par divers récits, qui sont autant de fictions ou de recréations imaginaires. Ces récits s’efforcent d'apporter une réponse à une énigme historique, qui est l’ « expérience cruciale » ayant permis cette découverte. La plupart décrivent des expériences dont le principe est scientifiquement correct, mais commettent des erreurs dans l’application du raisonnement. Le fait à retenir pour nous est que la découverte de Pythagore ait donné lieu, dès la plus haute antiquité, à une multitude de « descriptions d’expériences possibles », qui sont typiques du style et des conventions de la physique moderne. Hypothèses en forme d'équations ou de généralisations mathématiques, protocoles d'expériences reproductibles, basés sur la mesure de grandeurs physiques : on peut dire que l’invention de Pythagore inclue à titre d'incidente celle de la physique mathématique elle-même. Si Pythagore n'a pas désigné lui même un experimentum crucis, chargé d'en illustrer le principe, c'est en réalité sans importance, parce que son équation constituait en elle-même un programme d’expérimentation évident et multiple : rapport entre la hauteur d’un son et la longueur d’une corde, le poids d’un maillet, etc. Qu'elles aient eu une base réellement expérimentale - car il y en eut -, ou qu'elles fussent seulement théoriques et fictionnelles, comme celle qu'on va lire, les spéculations des pythagoriciens dans les domaines de l'harmonie et de l'acoustique, se signalent par leur direction scientifique, étrangère à l'esprit de l'antiquité : notamment par leur compréhension du phénomène du son, dont la nature vibratoire, voire ondulatoire, était déjà soupçonnée.*
L'un de ces récits, donc, rapporté par plusieurs auteurs antiques et médiévaux, raconte que Pythagore, passant près d’une forge, fut charmé et surpris par les sons de marteaux de différents poids frappant sur une enclume. Il pesa les marteaux et trouva que ceux-ci pesaient respectivement 6, 8, 9 et 12 unités de poids. En rapportant ces nombres à 6, on obtient les fractions suivantes (réduction en facteurs premiers) :
6 8 9 12
1 4/3 3/2 2
Qui sont respectivement l’unisson, la quarte, la quinte et l’octave.
(Précisons que l'expérience ici décrite est incorrecte en ce que, dans le cas de marteaux de différents poids, les rapports corrects ne s'appliquent pas à des nombres entiers, mais aux racines carrées de ces nombres. D'autres récits décrivent des expériences correctes, comme celle prêtée à Hippase sur des disques de bronze de différentes épaisseurs; d'autres encore appliquent le même raisonnement à des cordes de longueurs différentes, ou encore à des vases remplis de différentes quantités d'eau.)
Ce système permet de définir tous les rapports musicaux en n’utilisant que les 4 nombres de la tétractys.
Mais là encore, nous devons remarquer que ces nombres se déduisent de la tétractys d'une manière bien particulière. Non seulement les nombres qui composent les fractions sont les nombres de la tétractys, mais, en disposant les 4 rapports dans cet ordre : 1, 2, 3/2, 4/3, on s’aperçoit que la tétractys est exprimée de manière génétique, puisque ces quatre rapports correspondent, respectivement, au rapport de la première ligne de la tétractys avec elle-même (1 ou 1/1), au rapport de la seconde ligne à la première (2, ou 2/1), au rapport de la troisième ligne à la seconde (3/2), enfin, au rapport de la quatrième ligne à la troisième (4/3).

Supersymétrie des accords musicaux et des objets premiers. **
Conclusion : les rapports arithmétiques qui sont ceux des quatre accords fondamentaux de l'harmonie musicale, (unisson, octave, quinte, quarte), correspondent, biunivoquement, aux rapports qu'entretiennent entre eux les quatre objets premiers de la géométrie, (point, segment, triangle équilatéral, tétraèdre), quant au nombre de points qui les composent ou, ce qui revient au même, quant au nombre de sommets qu'ils comportent.
Unisson Octave Quinte Quarte
1/1 2/1 3/2 4/3

Dans cette application, les objets premiers de la géométrie apparaissent donc, relativement aux accords musicaux, comme des réalités moins primitives, mais en quelque sorte dérivées, puisqu'ils expriment dans leurs rapports mutuels ce que les accords musicaux expriment en eux-mêmes.
L'idée que l'espace et le temps sont des réalités qui ne peuvent se développer que de manière symétrique et coordonnée, est une idée dont on trouve d'autres illustrations dans la littérature pythagoricienne.
Dans les articles suivants, nous verrons que ces rapports musicaux permettent en outre de définir les trois médiétés classiques qui, dans la tradition, jouent le rôle de noyau logique du système complet des 12 médiétés; à savoir la médiété « arithmétique », la médiété « géométrique », et la médiété « harmonique » .
*Contrairement à un préjugé répandu, qui voudrait que la doctrine pythagoricienne ait entretenu une certaine confusion entre les plans mathématique et physique, toutes les expériences que nous rapporte la tradition montrent un étagement correct des niveaux ontologiques : mathématique / physique et hypothèse / expérience. Archytas : "Les sons sont causés par la vibration de l'air. Les sons aigüs correspondent à des mouvements rapides, les sons graves à des mouvements lents." Selon le sentiment de plusieurs historiens de la physique, la première grandeur physique qui soit caractéristique du style et des procédures de la physique moderne, n'est autre que la vitesse archytéenne, qui est, dans toute sa rigueur mathématique, et avec son réel horizon expérimental : la vitesse de vibration de l'air correspondante à la hauteur d'un son. Georges Mourier, historien de la physique ondulatoire, a ainsi montré que la théorie moderne du son se déduisait très naturellement des opérateurs mathématiques mis en oeuvre par Archytas et ses congénères.
** Nous empruntons le terme contemporain de "supersymétrie" pour désigner ce qui est ici, très simplement, une symétrie entre deux symétries, - entre deux séries d'objets dont le principe générateur individuel est déjà une symétrie.
-
LES TROIS MEDIETES DE LA THEORIE CLASSIQUE
A la fin de son Introduction arithmétique, et comme en couronnement de ce livre, Nicomaque qualifie de "médiété parfaite" la série harmonique (6 - 8 - 9 - 12), dont l'importance dans la mathématique pythagoricienne est telle, qu'elle a reçu le nom de "grande tétractys". Récemment, certains auteurs se sont même enthousiasmés à voir en elle la tétractys la plus ancienne ou la plus originelle, mais ces hypothèses historiques, au demeurant aussi gratuites que possible, n'ont pas d'intérêt pour les véritables pythagoriciens, puisqu'on a vu que cette grande tétractys n'était qu'une simple application, qu'un simple développement mathématique de la tétractys « classique ».
La perfection de la série harmonique (6 - 8 - 9 - 12), tient à ce qu'elle contient les rapports des trois médiétés que la tradition définit comme "premières en naissance"; et l'on sait déjà l'importance de ce critère en pythagorisme. Cet article sera consacré à illustrer cette primauté généalogique des trois premières médiétés sur les suivantes; et nous verrons au passage comment elles se déduisent de la série harmonique de la grande tétractys. On s'efforcera ensuite, dans les deux articles suivants, de traiter du système complet des médiétés.
Comme la théorie du gnomon, l’étude du système des médiétés est un domaine encore peu exploré de la mathématique. Le nombre même de ces médiétés est une question problématique, et fait l’objet d’un flottement selon les auteurs : 10 selon Nicomaque de Gérase, 12 selon Théon de Smyrne, 11 pour la plupart des auteurs récents qui ont tenté de donner une définition moderne de ce système. Nous montrerons ici que la détermination exacte du nombre des médiétés dépend de l’ensemble arithmétique dans lequel on les définit. En effet, s’il y a bien 11 médiétés dans N* (l’ensemble des entiers naturels, sauf zéro), il y en a 12 dans N (l’ensemble des entiers naturels, inclu zéro), conformément à la conjecture de Théon de Smyrne. Dans cette étude, on appelle « Nicomaque 1 à 10 » les 10 médiétés recensées dans le catalogue de cet auteur, et « Théon 11 et 12 » les deux qui ont dû leur être ajoutées. Nous donnons, à la fin de cette première section, une table des médiétés, à laquelle le lecteur pourra se reporter selon ses besoins.
En réalité, seules les trois premières de ces médiétés, qui sont les médiétés immédiatement déductibles des rapports arithmétiques de la grande tétractys, ont fait l’objet, - et ce, dès l’antiquité - d’une étude vraiment détaillée. A ces trois médiétés classiques on peut ajouter la médiété Nicomaque 10, qui a fait l’objet d’un intérêt plus récent, en raison de sa relation avec la célèbre « suite de Fibonacci ».
*
Définitions
René Taton.
"Une médiété est un rapport entre trois termes, tel que deux d'entre eux et deux de leurs différences soient dans le même rapport."
Cette définition peut être transformée en une définition purement logique et formelle, sans contenu sémantique. Par exemple :
Une médiété est une expression à six places vides de la forme ci-dessous, dans laquelle les relations arithmétiques entre les termes sont constantes, et où les six places doivent être remplies par les lettres a, b, c, telles que a < b < c.
(...) - (...) = (...)
(...) - (...) (...)
Enfin, les relations arithmétiques entre les termes étant supposées connues, il est possible, comme nous le verrons dans la partie démonstrative de cet exposé, de réduire le problème des médiétés à celui d'un tableau à six cases (logon), où les cases doivent être remplies par les lettres a, b et c.
a
a
a
a
a
a
De telles définitions ne sont bien sûr pas complètes, puisque, si toutes les médiétés sont des expressions de cette forme, toutes les expressions de cette forme ne sont pas des médiétés. En effet, le total des solutions possibles pour cette formule est de 36 = 729, entre lesquelles un petit nombre seulement, de dix à douze selon les auteurs, sont des médiétés.
Nous appellerons ici mineure la partie de l'expression située à droite du signe égal, concernant des termes simples (a, b, ou c) et majeure celle située à gauche du signe égal, concernant des différences entre ces termes, et conviendrons de placer toujours la majeure devant la mineure, comme ci-dessus.
Nous présenterons les 6 premières médiétés dans leur ordre traditionnel, qui est d'ailleurs l'expression d'une réalité structurelle que nous traiterons en son lieu. La documentation sur les 3 premières médiétés est assez abondante, et, ne pouvant les traiter de façon exhaustive, nous favoriserons ici, en fonction des besoins qui sont les nôtres, d'une part, les éléments de description qui permettent d'extraire des médiétés un contenu intuitif ou intellectif, d'autre part, les éléments permettant de dégager les aspects topologiques et structurels du système des médiétés.
Comme il n'entre pas dans notre propos d'étudier la place des médiétés dans l'histoire de la philosophie, on se contentera, ici, de citer quelques exemples. Platon, dans le Timée, recourt à la médiété géométrique pour construire son échelle harmonique de l'âme du monde. Aristote, dans son Ethique à Nicomaque, utilise la même médiété pour exposer le principe économique de la justice et de l'égalité. Fibonacci montre, lui, comment on peut utiliser la médiété 10 pour décrire la croissance d'une population de lapins; et c’est un peu dans le même esprit que Malthus, dans son célèbre théorème économique, énonce que la population humaine s'accroît en moyenne géométrique, alors que ses ressources ne s'accroissent qu'en moyenne arithmétique.
Evoquons une question de vocabulaire. L'usage d'appeler "arithmétique", "géométrique" et "harmonique" les 3 premières médiétés est traditionnel. Il est déjà présent chez Archytas, et a même reçu chez Nicomaque une justification étendue. Quelle que soit l'ancienneté de cet usage, il nous paraît, à nous, plutôt de nature à engendrer la confusion. Les 3 médiétés renferment chacune des aspects arithmétiques, géométriques et harmoniques; ces appellations ne sont donc pas décisives pour comprendre leurs propriétés principales, du moins au point de vue qui est le nôtre.
Bien que la tradition attribue à Pythagore la découverte des 3 premières médiétés, la première recension écrite de ces médiétés se trouve dans l'oeuvre d'Archytas de Tarente. Pour ces trois médiétés, nous donnerons à chaque fois en ouverture la définition d'Archytas.
La médiété arithmétique
Archytas :
"En musique, il existe trois médiétés : arithmétique, géométrique et subcontraire, encore appelée harmonique.
"On parle de moyenne arithmétique, quand trois termes entretiennent entre eux une proportion selon un excès donné, et que l'excès du premier par rapport au deuxième est celui du deuxième par rapport au troisième."
Précisons que nous suivons ici l'usage moderne, de préférence à celui d'Archytas, et désignons comme "le premier" (a) le plus petit des trois termes, et appelons "c", ou "troisième", le plus grand des trois termes.
Cette médiété se note :
b - a = a ( = b = c ) ( = 1)
c - b a b c
avec : a < b < c
Et sa plus petite solution possible pour (a, b, c) est (1, 2, 3)
L'exemple le plus simple que l'on puisse trouver est donc celui de la suite des entiers naturels : 1, 2, 3, 4, 5, ....
Commençons par détailler quelques propriétés de cette médiété.
On a :
c - b = b - a
b = a + c
2
c = (b - a) + b
c = 2b - a
Si l'on prend la chaîne des entiers naturels, on constate que l'on peut appliquer à n'importe quel endroit de cette chaîne un objet logique en forme de trident, correspondant aux termes a, b, c; en vertu de quoi tout triplet de nombres successifs choisis dans cette chaîne satisfait la médiété "Nicomaque 1", ou médiété "arithmétique".
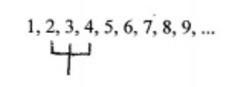
Mieux encore, cet objet logique, le trident, peut être affecté d'un vecteur de croissance indéfinie, de manière à pouvoir sélectionner cette fois des termes non voisins de la chaîne, à la seule condition que la croissance du trident soit uniforme, c'est-à-dire, que l'égalité entre les deux sous-intervalles soit continuellement maintenue.

Résumons les aspects les plus originaux de la médiété arithmétique.
- Dans cette médiété, le rapport mineur a une valeur constante : 1. Cette particularité est propre à la médiété Nicomaque 1 à l'exclusion de toutes les autres.
- Dans sa solution la plus simple (1, 2, 3), cette médiété a une signification intuitive qui est l'opération "+1", qui engendre la chaîne des entiers, et qui est aussi l'explication de son qualificatif d'arithmétique.
- Dans son application par la croissance du trident, cette médiété a une signification intuitive qui est la continuité, à toutes les échelles du nombre, de la fonction d'intervalle régulier. La croissance du trident est tout simplement la croissance endomorphe de la fonction arithmétique d'intervalle régulier, qui, partant d'une portion atomique ou entière d'intervalle, s'étend ensuite, par une progression continue, à toutes les dimensions pouvant contenir celle-là, comme une partie. A partir d'un intervalle minimum, sommet d'un cône topologique, est défini le principe de la croissance illimitée de cet intervalle.
- Ajoutons une dernière singularité. La médiété Nicomaque 1 est la seule à comporter 3 fractions du côté de la mineure. Une autre médiété, la médiété Nicomaque 2, comporte 2 fractions, tandis que les dix autres ne comportent qu'une seule fraction.
Ces précisions nous serons utiles lorsque nous aurons à analyser le sous-système constitué par les 3 premières médiétés.
La médiété géométrique
Archytas :
"On parle de moyenne géométrique, quand le rapport des trois termes est tel que le premier est au deuxième ce que le deuxième est au troisième."
Des exemples courants de cette médiété sont les proportions que nous appelons communément "double", "triple", "quadruple", etc.
Ainsi, la série suivante (double) :
1, 2, 4, 8, 16, 32, 64, 128, ...
Ou encore la série suivante (triple) :
1, 3, 9, 27, 81, 243, ...
On voit que le domaine d'application de cette médiété est, comme celui de la précédente, d'une grande généralité mathématique, puisque les rapports tels que "double", "triple", dont la liste est évidemment infinie, peuvent, chacun à son tour, être appliqués à tout nombre n, comme on vient de le faire ici au seul nombre 1.
Cette médiété se note :
b - a = a ( = b )
c - b b c
et sa plus petite solution possible pour (a, b, c) est (1, 2, 4).
Pour cette médiété, on a, outre la définition d'Archytas, celle du Timée de Platon.
(On parle de moyenne géométrique), "chaque fois que, de trois nombres quelconques, que ces nombres soient entiers ou en puissance, celui du milieu est tel que ce que le premier est par rapport à lui, lui-même l'est par rapport au dernier, et inversement, que ce que le dernier est par rapport à celui du milieu, celui du milieu l'est par rapport au premier, le dernier et le premier pouvant à leur tour devenir moyen."
C'est cette médiété qui sera mise en oeuvre ensuite dans la célèbre construction arithmétique et musicale de l 'âme du monde
Nicomaque, quant à lui, nous introduit à cette médiété par une voie apparemment détournée, qui est de la considérer d'abord comme un problème à 4 termes, pouvant ensuite être ramené à 3 termes. Cette voie d'exposition étant assez intellective, nous nous y attarderons un instant.
Si nous considérons des séries familières telles que les rapports : « double », « triple », etc :
1, 2, 4, 8, 16, ...
1, 3, 9, 27, ...
On observe que :
a/b = c/d = e/f = ...
Ce qui, pour la série double, donne :
1/2 = 4/8 = 16/32 = ...
Et pour la série triple :
1/3 = 9/27 = 81/243 = ...
Si nous exprimons maintenant cette application comme une fonction "en trident", cela revient à dédoubler la barre centrale du trident, de façon à inclure désormais quatre termes dans la relation, soit :

Où : 1/2 = 4/8 = ...
La médiété devient alors une fonction qui relie des termes successifs par paires, exprimant que chacune des fractions composées d'une de ces paires est égale à la suivante et à toutes les suivantes.
Mais n'oublions pas que le rapport "trident" qui est présenté ci-dessus sous une forme "disjointe", peut être ramené à une forme "conjointe", donc à un trident simple, puisque la proportion qui court dans les intervalles - les "trous" de la chaîne ci-dessus - est également la même. En effet :

Les rapports : 2/4, 8/16, ..., correspondant à ces "jointures" supérieures sont eux mêmes égaux à ceux de la chaîne inférieure.
Notons qu'à partir d'une suite de termes étendue telle que :
a b c d e f g h
on peut former des équations telles que : a/d = e/h, ou encore a/c = b/d. Les segments peuvent croître indéfiniment, ou se croiser, pour peu qu'il soient toujours de même longueur.
Pour conclure, remarquons une propriété de cette médiété, qui peut éclaicir le contenu sémantique de celle-ci; de la même manière que nous avions reconnu dans la première médiété un contenu sémantique qui est la constance, à toutes les échelles du nombre, de la fonction d'intervalle régulier.
Dans cette médiété, on a : ac = b2
par exemple 1 x 4 = 22, etc, dans la série "double".
ou 1 x 9 = 32, etc, dans la série "triple".
Une façon de comprendre cette médiété peut donc consister à transformer l'équation ac = b2 en un axiome d'existence, postulant que tout carré d'un nombre n (le terme médian "b"), tel que n > 1, peut s'exprimer comme le produit de deux nombres, l'un inférieur, l'autre supérieur à n (les termes extrêmes a et c).
La médiété peut, de cette manière, être lue comme une conjecture ou un théorème mathématique qui serait le suivant :
Pour tout b > 1, il existe une paire (a, c) telle que a < b < c, et telle que ac = b2. La preuve de ce théorème est du reste aisée à produire, puisqu'on peut montrer que pour tout nombre b supérieur à un, il existe au moins un couple de ce genre, qui est le couple (1, b2), où l'on a bien a < b < c. La formule ac = b2 prend simplement, dans cette formulation, la place de la formule "constructive", dont notre médiété dérive par extension.
A ces quelques remarques, on peut ajouter que les concepts de "double" et de "triple", qui découlent des premières applications de cette médiété, ont fait l'objet, dans l'antiquité, d'amples spéculations géométriques, comme dans le fameux problème de la duplication du cube, ce qui peut expliquer son appellation traditionnelle de médiété géométrique.
La médiété harmonique
Archytas :
"On parle de moyenne subcontraire, celle que nous appelons harmonique, quand le rapport de trois termes est le suivant : le premier terme dépasse le deuxième d'une fraction de lui-même et le moyen dépasse le troisième de la même fraction du troisième. "
Cette médiété se note :
b - a = a
c - b c
et ses plus petites valeurs possibles pour (a, b, c) sont (2, 3, 6).
D’autres auteurs anciens, tels que Platon ou Nicomaque, ont également défini cette médiété, et ont fait remarquer, comme Archytas, que la médiété harmonique entretient une relation directe avec la médiété arithmétique, puisqu’elle n’est autre qu’une moyenne arithmétique entre inverses.
En effet, il est assez simple de démontrer mathématiquement que des termes (a, b et c) sont en moyenne harmonique si et seulement si leurs inverses sont en moyenne arithmétique.
Cette remarque doit maintenant nous faire entrer dans des remarques structurelles.
Structure des médiétés 1, 2, 3
La médiété harmonique découle de l'arithmétique en prenant les inverses des termes de celle-ci, par quoi on la désigne du nom de sous-contraire ou subcontraire.
Ici se place un petit problème de vocabulaire. L'expression "sous-contraire", qui désigne la relation entre une fraction et son inverse, va devenir, après Archytas, une sorte de mot-valise, exprimant l'idée qu'à partir de la médiété Nicomaque 1, on peut retrouver toutes les autres, à ceci près que la relation d'inversion n'est pas appliquée aux mêmes endroits de la médiété. Selon les auteurs, l'expression "sous-contraire" désigne une formule pouvant être obtenue à partir d’une autre, soit en prenant les inverses de ses termes, soit en prenant les inverses de l'une ou l'autre des fractions qu'elle contient. La signification du terme "sous-contraire" s'élargit même en deux temps, de sorte qu'après avoir désigné, à partir d'Archytas, la relation de la médiété 3 à la médiété 1, il désignera, chez Théon de Smyrne, la relation du sous-ensemble des médiétés 4 à 6 à celle du sous-ensemble 1 à 3, et enfin la relation du sous-ensemble 7 à 12 au sous-ensemble 1 à 6. A y regarder de près, ces emplois du terme sous-contraire ne sont pas incompatibles, puisqu'ils délimitent des parties distinctes, mais complémentaires du système des médiétés.
Parallèlement à cette liaison entre les médiétés 1 et 3, on trouve chez de nombreux auteurs l'idée que les médiétés 1, 2 et 3 constituent une structure indépendante.
Commençons par nous faire une idée de la nature de cette "triangularité" qui est réalisée dans le sous-système des médiétés 1 à 3, formant le noyau logique du système général. Les trois médiétés sont identiques dans leur partie majeure, et ne se distinguent que par leur partie mineure. Le système de leurs différences doit donc trouver son expression dans le système de variation de la fraction mineure. Pour le saisir, il nous faut faire subir à cette fraction une rotation de 90 degrés, pour l'amener à représenter ce qu'elle est effectivement : un intervalle sur la chaîne, conventionnellement horizontale, des entiers. De cette manière, on s'aperçoit que, dans la médiété Nicomaque 1, cet intervalle est le minimum, puisqu'il est nul :
a / a (intervalle de rang zéro)
Tandis que, dans la médiété Nicomaque 3, cet intervalle est l'intervalle maximum, puisqu'il est l'intervalle entre les deux extrêmes:
a / c (intervalle de rang 2)
L'observation de ces deux formules permet donc de trouver déductivement la troisième, qui n'est autre que la formule intermédiaire entre les deux autres, où de ce fait l'intervalle est "moyen".
a/b (mais aussi b/c) (intervalles de rang 1)
Nous disons l'intervalle, mais il s'agit bien dans cette médiété Nicomaque 2 de deux intervalles a/b et b/c; de sorte qu'au triangle formé par la croissance de l'intervalle de la fraction mineure de la médiété

A cette structure donc s'oppose une structure en triangle qui est l'inverse de celle-là, et qui est celle du "nombre de fractions dans la partie mineure".
Médiété 1 : 3 fractions (a/a b/b c/c)
Médiété 2 : 2 fractions (a/b b/c)
Médiété 3 : 1 fraction (a/c) Décroissance du nombre de fractions
Une réflexion un peu attentive fera comprendre que cette seconde structure est un corrélat de la première, de sorte qu'on a affaire à deux structures triangulaires qui sont réciproques et duales l'une de l'autre.
Concernant cette double propriété de la triade des médiétés Nicomaque 1 à 3, de constituer à la fois le noyau et la matrice de toutes les suivantes, en même temps qu'un système achevé et clos sur lui-même, nous devons nous rappeler que ces trois médiétés sont celles qui se déduisent des rapports arithmétiques de la "grande tétractys" (6 - 8 - 9 - 12).
Comme l'a montré Nicomaque, alors que les termes 6, 9, 12 sont en proportion arithmétique, les termes 6, 8, 12, sont eux, en proportion harmonique.

Quant à la médiété géométrique, elle s'obtient, elle, par alternation des rapports 6 - 9 et 8 - 12.

Articulation de l'ensemble des médiétés 1 à 3 à celui des médiétés 4 à 6
A présent, le système triangulaire dont nous venons d'exposer les caractères de complétude et de clôture, ce système se définit aussi comme un sous-ensemble, au sein d'un ensemble de rang supérieur, comprenant, celui-là : "toutes les formules qui ont pour majeure la sous-formule (b - a) / (c - a)".
Cette définition du sous-ensemble des médiétés 1 à 6, notons le, nous renvoie déjà à la question de la clôture du système des médiétés, puisque nous verrons que le sous-ensemble des 6 médiétés restantes (de 7 à 12), pourra lui-même être défini comme l'ensemble des médiétés qui n'ont pas pour majeure la formule (b - a) / (c - a).
On voit que, dans cette situation gnoséologique particulière, l'hyper-ensemble, le système complet, est construit déductivement à partir de l'ensemble-noyau, par la simple considération de ce qui lui manque. Le système qui nous occupe à présent comprend 6 éléments, et la déduction des trois premières médiétés aux trois suivantes se fait, comme de coutume, par la mise en oeuvre d'un opérateur de "sous-contrariété".
En effet, les médiétés 4 à 6 sont des sous-contraires, de médiétés (ou plus exactement, comme on va le voir, de formules de médiétés) appartenant au groupe 1 à 3. Le "triangle" des médiétés (1-2-3) se voit doté d'un complément triangulaire, dont les éléments se déduisent des éléments du premier groupe en inversant les deux termes de la fraction mineure.
Mais que devons-nous remarquer tout de suite?
Que cette relation, la sous-contrariété, n'est pas biunivoque, mais comporte une dissymétrie. En effet :
a) La médiété 1 n'a pas de sous-contraire, puisqu'en inversant les termes de la fraction a/a on n'obtient pas une nouvelle formule, mais la même formule.
b) La médiété 2 possède deux sous-contraires, qui ne sont pas des propriétés distinctes d'une même médiété, mais bel et bien deux médiétés distinctes, dont les solutions sont différentes.
c) La médiété 3 ne possède qu'une sous-contraire.
Nous sommes à présent en mesure de reporter tout ceci sur un schéma topologique continu, dans lequel le triangle intérieur des médiétés (1-2-3) est la matrice du triangle des médiétés (4-5-6).
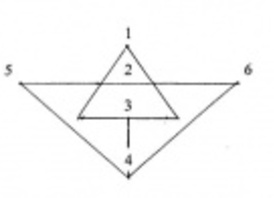
Remarquons toutefois que, pour exprimer cette relation topologique, on doit consentir à ce que la représentation de la médiété ne soit pas la même, dans le triangle (1-2-3) et dans le triangle (4-5-6). En effet, dans le triangle intérieur, une médiété est représentée par un segment (de longueur nulle pour la médiété 1), tandis que, dans le triangle extérieur, une médiété est représentée par un point topologique
Avant d'aborder, dans le prochain article, la partie démonstrative de cet exposé, faisons le point sur la question du développement historique de la théorie des médiétés. L'analyse structurale que nous venons de mener sur les médiétés 1 à 6 constitue un socle ancien et stable, que l’on trouve autant en accord avec Théon qu'avec Nicomaque. Mais à partir de là, tout change. Théon nous annonce 12 médiétés, les 6 dernières devant être une fois de plus les "sous-contraires" des 6 premières; mais, hélas, il ne nous détaille réellement que les médiétés 1 à 3. Nicomaque nous présente une "décade de médiétés", ce qui a très tôt éveillé un soupçon qui s'exprime ainsi : que vient faire ici la décade?
C'est à la question de la complétude du système des médiétés et à la détermination rigoureuse de leur nombre que sera consacré le prochain article.
-
LE SYSTEME DES 12 MEDIETES
(démonstration de complétude)
L'objet de cet article est de démontrer que, conformément à la conjecture de Théon de Smyrne, il existe 12 médiétés, mais en outre, qu'il ne peut en exister davantage.
On verra que la résolution du système, ou sa clôture, en onze ou en douze médiétés relève, en ultime instance, d'une situation de choix, qui équivaut à définir le système des médiétés ou bien dans N* (N sauf zéro) ou bien dans N (inclus zéro ou l'ensemble vide). Nous verrons néanmoins que l'adoption de la 12e médiété est recommandée par la symétrie interne du système, au sein duquel cette médiété se réduit à un énoncé qui n'est autre qu'un axiome d'existence du nombre zéro.
Commençons par présenter notre méthode de démonstration.
Dans un premier temps, le problème des médiétés est défini sur un plan strictement logico-formel, qui est celui que nous avons déjà énoncé plus haut :
"Une médiété est une expression à 6 places vides de la forme :
(...) - (...) = (...)
(...) - (...) (...)
dans laquelle les relations arithmétiques sont constantes, et où les six places vides doivent être remplies par les lettres a, b, c, telles que : a < b < c."
Cette définition permet de paramétrer le champ topologique complet du système des médiétés, défini par l'ensemble, intégralement coordonné, de "toutes les formules possibles de ce modèle". Cet ensemble est composé de 36 = 729 éléments.
Lorsqu'on saisit dans cette jungle de formules une formule particulière pour l'examiner dans le détail, il va se produire très souvent (en fait, dans presque tous les cas) que cette formule s'élimine d'elle-même, entraînant dans sa chute d'autres formules du même modèle, par la simple considération de sa signification.
On appelle ici "méthode des cribles" cette méthode de balayage du champ amorphe des formules logoniques, par des moyens sémantiques, issus de l'analyse du sens des propositions. Alors que les planches logoniques I à IX nous donneront de la médiété une image purement formelle et syntaxique, les cribles successifs appliqueront sur ce champ logonique une analyse localisée, formule par formule. Ces cribles considèrent le sens de certaines formules, et, ayant reconnu ce sens comme contraire à la définition d'une médiété, ou bien manifestement faux, ou bien redondant avec une autre formule, éliminent à la suite toutes les formules analogues à la formule incriminée.
La méthode des cribles permet de définir ce qu'est une médiété d'une façon qui est entièrement mathématique, bien que sa forme soit en apparence négative. Les médiétés se trouvent à la fin définies comme les formules qui restent, une fois actionnés l'un après l'autre la totalité des cribles. Néanmoins, cette définition négative peut être "retournée", c'est-à-dire comprise positivement. Une médiété se trouve définie comme une formule n'ayant aucune des propriétés énumérées par les cribles. La définition est mathématiquement complète en ce que :
1. Aucune des 12 médiétés n'a l'une ces propriétés,
2. Seules entre toutes les formules de médiétés, ces 12 ont la propriété de n'avoir aucune de ces propriétés.
Ou bien, synthétiquement : toutes ces formules (de 1 à 12), et seulement elles, ont la propriété de n'avoir aucune de ces propriétés.
Les formules échappant à la succession des cribles se voient ainsi définies comme constituant le système complet des médiétés pythagoriciennes, en tant que système des seules médiétés possibles, résultantes.
Notre programme sera le suivant :
- On introduit un crible initial qu'on appelle le crible zéro, qui permet de passer de 729 formules à 144, à la suite de quoi on expose le principe selon lequel sont construites nos 9 planches logoniques
- On introduit les cribles 1 à 8 en tenant le compte exact des formules éliminées au fur et à mesure.
- On donne à la suite les 9 planches logoniques sur lesquelles s'effectuent ces opérations, planches sur lesquelles sont indiquées, pour chacune des 132 formules éliminées, l'intitulé du crible au nom duquel elle a été supprimée.
- Enfin notre enquête se conclut par quelques remarques finales sur la structure du système des médiétés, ainsi que sur le statut particulier de la médiété Théon 11.
Le crible zéro et la structure des planches logoniques I à IX.
Nous commençons par énoncer une définition de la médiété plus restrictive que celle, purement formulaire, qui nous a servi jusqu'ici, et cette définition nous permettra ensuite d'actionner, non seulement le crible zéro qui nous occupe ici, mais un autre par la suite (le crible 4), en partant du fait qu'un certain nombre de formules ne correspondent pas à cette définition restrictive de la médiété.
Définition :
"Une médiété est une égalité de rapports entre des différences positives et non nulles (majeure), et des nombres positifs et non nuls (mineure). Ou bien, pour parler mathématiquement :
Une médiété est une expression de la forme :
x = a
y b
dans laquelle x, y, a et b sont des nombres positifs supérieurs à zéro.
Dans le contexte qui est celui du pythagorisme, où le zéro, aussi bien que les nombres négatifs, sont réputés n'avoir pas d'existence, une telle limitation, - qui est naturellement respectée aussi bien dans les 10 médiétés de Nicomaque que dans la 11ème qui lui a été ajoutée par les commentateurs modernes, - une telle restriction n'apparaîtra pas abusive, mais bien plutôt, elle nous semblera pointer une propriété implicite de ce que nous comprenons, dans ces 11 exemples, comme étant une médiété.
Cette nouvelle définition permet de supprimer un grand nombre de formules, et notamment toutes celles (crible zéro) qui, dans leur partie majeure, contiennent une différence de type (a - b) ou encore (b - c), autrement dit une différence où le terme le plus petit précède le plus grand, et dont le résultat est, de ce fait, négatif. Notre définition de la médiété n'admettant que des différences positives, toutes les formules de ce type ne sont pas autorisées.
Il nous faut ici définir avec précision les limites exactes introduites par cet axiome. Notre définition n'oblige pas par exemple les éléments (a, b ou c) intervenant dans la majeure à être non nuls, mais seulement les différences entre ces éléments. Par contre, du côté de la mineure, les éléments doivent être non nuls, c'est à-dire qu'un terme (a, b ou c) figurant dans la mineure, ne peut pas être égal à zéro. Cette précision aura toute son importance lorsque nous aurons à examiner le statut particulier de la médiété Théon 11.
Examinons maintenant plus en détail la situation combinatoire - ou logonique - déterminée par l'actionnement du crible zéro.
Alors qu'auparavant nous avions, pour chaque case du diagramme, trois solutions possibles, (a, b ou c), la somme de ces solutions étant dès lors égale à 36 = 729 formules, ne sont plus permises désormais, dans chacune des cases du logon à 6 places, que les solutions suivantes :
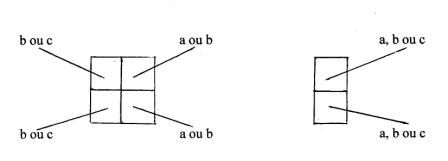
Soit en tout : 2 x 2 x 2 x 2 (= 16 ) x 3 x 3 = 144 formules seulement.
Cette analyse nous permet d'expliciter la structure de nos 9 planches logoniques.
La formule majeure constitue un système combinatoire autonome comportant 16 solutions seulement. Ces 16 solutions sont développées identiquement sur chacune des planches de notre logothèque : ce qui signifie que nos 9 planches sont identiques pour ce qui est de la formule majeure et ne différent entre elles que par la mineure. Ces neuf planches correspondent tout simplement aux 9 solutions possibles (3x3) pour le "remplissage" de la mineure soit : (a/a, b/b, c/c, a/b, b/a, a/c, c/a, b/c, c/b).
Ce qui nous donne bien, au total 16 x 9 = 144 formules
Ces précisions nous permettent en outre d'attribuer à chaque formule un numéro d'ordre à deux coordonnées, de type (II, 4), dans lequel le chiffre romain indique le numéro de la planche (qui permet donc de retrouver sa formule droite ou mineure), et le chiffre arabe son rang dans le développement de 1 à 16 de la partie majeure.
C'est donc sur ce champ logonique réduit que vont désormais s'appliquer les 8 cribles successifs énumérés ci-après.
Sur les 729 formules dont nous disposions au départ, le crible zéro a supprimé toutes les formules contenant une différence négative, de forme (a - b), (a - c) ou (b - c), mais aussi les deux tiers des formules contenant une différence nulle (les formules en (a - a) et (c - c)). Seules les différences nulles de la forme (b - b) ont résisté au crible zéro, puisque notre diagramme prend en compte uniquement les solutions possibles pour chacune des cases du tableau, sans préjuger de ce qui figure sur une autre case du même tableau; or, la lettre b est la seule à être possible sur chacune des 6 cases du diagramme, contrairement aux lettres a et c. La suppression des formules contenant l'expression (b - b) devra donc faire l'objet d'un crible spécial ultérieurement (crible 4).
Crible 1 : « Ne contient pas trois lettres »
Une médiété est un rapport entre trois termes (a, b, c)
Sur nos 144 formules, le critère : "cette formule ne contient pas trois lettres, est n'est donc qu'une relation entre - au maximum - deux éléments" - ce critère permet d'éliminer 34 formules.
Restent 144 - 34 = 110 formules.
Crible 2 : « Formule miroir »
On peut éliminer toutes les formules dans les quelles le haut et le bas (de la formule) sont identiques.
Prenons par exemple la formule :
b a c
b a c, qui se lit :
(b - a) = c
(b - a) c
Le sens de cette formule n'est qu'une pure évidence mathématique qui énonce :
x/x = y/y (=1)
En tout état de cause, cette formule n'énonce pas une relation déterminée entre trois termes réciproquement définis, mais une évidence mathématique valable indistinctement pour tout nombre n.
Ce critère élimine quatre nouvelles formules. Restent 110 - 4 = 106 formules.
Crible 3 : « Image de (..., ...) »
On peut supprimer toutes les formules qui peuvent être obtenues à partir d'une autre formule, en inversant le haut et le bas.
Par exemple la formule :
b a c
c b a
Cette formule peut-être obtenue à partir de la formule :
c b a
b a c en inversant les lignes du haut et du bas.
En réalité, ces deux formules ne sont pas deux formules différentes, mais l'une n'est qu'une conséquence mathématique triviale de l'autre, en vertu de l'évidence selon laquelle :
si (a/x) = (b/y) alors (x/a) = (y/b)
Autrement dit, nous n'avons pas affaire à deux formules différentes, mais à deux expressions équivalantes de la même formule. Pour cette raison, l'une ou l'autre de ces formules peut indifférement être éliminée, et l'autre conservée comme un représentant valable de la formule considérée. Ici, on choisit arbitrairement de conserver la première qui apparaît dans notre liste.
Le critère "Cette formule est l'image de la formule (..., ...) permet à lui seul d'éliminer la moitié des formules subsistantes, ce qui laisse subsister 106/2 = 53 formules.
Notons en particulier que trois planches entières peuvent être rayées d'un seul trait de plume. En effet, la planche 5, par exemple, étant tout simplement l'image de la planche 4, peut être supprimée intégralement. Même chose pour les planches 7 et 9, qui sont respectivement les images des planches 6 et 8.
Crible 4 : « Contient une différence nulle »
Selon notre définition initiale d'une médiété, les différences entre deux termes qui figurent dans la majeure doivent être des valeurs positives et non nulles. Cette restriction a déjà permis d'éliminer, à l'occasion du crible zéro, toutes les formules dans lesquelles figurait une différence négative, ainsi que les formules contenant une différence nulle de la forme (a - a) ou (c - c).
A présent, la même restriction nous permet d'éliminer toutes les formules subsistantes où figure une différence nulle, de la forme (b - b), - formules qui, pas plus que les précédentes, ne sont permises par notre définition.
Le critère "Cette formule contient une différence nulle" permet d'éliminer 20 nouvelles formules, et il nous reste à ce stade 53 - 20 = 33 formules.
Crible 5 : « Faux 1 »
Examinons maintenant la formule Nicomaque 1, qui nous est familière :
( c - b ) = a ( = 1 )
( b - a ) a
Cette formule implique que ( c - b ) = ( b - a )
De la même manière, toutes les formules qui ont pour mineure une sous-formule du type ( x/x ) (= 1), impliquent que, dans la majeure, la différence du haut soit égale à la différence du bas.
Cette analyse permet dès lors d'éliminer un certain nombre de formules comme mathématiquement fausses.
En effet, toutes les formules dans lesquelles on a à la fois, dans la mineure, une fraction de type ( x/x ), et, dans la majeure, deux lettres identiques se situant sur une même verticale, toutes ces formules sont, de toute évidence, mathématiquement fausses.
Prenons par exemple la formule :
( c - a ) = a
( b - a ) a
Cette formule contient, dans sa mineure, une expression de la forme (x/x) (=1), et, dans sa majeure, deux lettres identiques sur une même verticale (a/a). Cela signifie que, pour que cette formule soit vraie, il faudrait tout simplement que b = c, ce qui est interdit par définition, puisqu'on a toujours b < c.
Ce critère "Faux 1" permet d'éliminer 6 nouvelles formules, et il nous reste à ce stade 33 - 6 = 27 formules.
Crible 6 : « Faux 2 »
Une autre famille de formules peuvent être reconnues fausses par hypothèse, les formules où l'on a en face d'une mineure de type (x/y) une majeure de type : (o - g) / (o - g)
soit une formule de la forme :
(o - g) = x
(o - g) y
Dont un exemplaire pris au hasard est la formule :
(c - a) = a
(c - a) b
Une telle formule est évidemment fausse. En effet, pour que cette formule soit vraie, il faudrait que a = b, ce qui est impossible, puisqu'on a par définition : a < b.
Ce critère élimine à son tour 6 nouvelles formules, et il nous reste à ce stade 27 - 6 = 21 formules.
Crible 7 : « Doublon de Nicomaque 1 ou 2 »
Notre connaissance particulière des médiétés Nicomaque 1 et Nicomaque 2 nous suggère ici l'idée d'un crible supplémentaire.
Nous savons qu'entre toutes les médiétés connues, la médiété Nicomaque 1 est la seule à comporter 3 fractions dans sa partie mineure, tandis que la médiété Nicomaque 2 est la seule à compter 2 fractions dans sa partie mineure, alors que toutes les autres médiétés connues ne comptent, dans leur partie mineure, qu'une seule et unique fraction.
Nous avons donc d'ores et déjà connaissance de trois formules qui ne sont pas des médiétés autonomes mais, pour les deux premières, ne sont autres que la médiété Nicomaque 1, bis et ter, et pour la troisième, la médiété Nicomaque 2 bis. Nous savons en effet que ces doublons particuliers ne correspondent pas à des médiétés différentes, mais à de simples variantes des médiétés susdites, ayant les mêmes solutions.
Ce critère nous permet donc d'éliminer 3 nouvelles formules.
Et il nous reste : 21 - 3 = 18 formules.
Crible 8 : « Faux 3 »
Examinons la formule :
( c - a ) = a
( c - b ) b
Par hypothèse ( c - a ) > ( c - b ) puisqu'on a : a < b.
Ce qui fait que nous avons là une formule qui énonce elle même les rapports suivants entre ses quantités :
(plus grand que dessous) = (plus petit que dessous)
(plus petit que dessus) (plus grand que dessus)
Cette formule est mathématiquement absurde, car le rapport d'un plus grand nombre sur un plus petit ne peut pas être égal à celui d'un plus petit sur un plus grand, pour la raison, tout simplement, que le premier est nécessairement supérieur à 1, tandis que le second est nécessairement inférieur à 1.
Ce critère permet d'éliminer 6 nouvelles formules, et les 12 formules qui nous restent constituent le système des 12 médiétés pythagoriciennes. CQFD.
Notre démonstration établit qu'il ne peut exister plus de 12 médiétés pythagoriciennes, puisque toute autre formule que ces 12 appartient à l'une ou l'autre des catégories de formules qui, pour ainsi dire, énoncent elles-mêmes qu'elles ne sont pas des médiétés, et ont pu sur cette base être éliminées sur des critères purement sémantiques. En outre, nous devons être bien convaincus d'avoir, par la méthode des cribles, parcouru la totalité du champ logique dans lequel s'inscrivent les médiétés; c'est-à-dire que nous savons réellement ce qu'énonce individuellement chacune des 717 formules éliminées depuis la mise en oeuvre du crible zéro.
-
TABLE DES MEDIETES
Nicomaque 1 Nicomaque 2
(b - a) = a (= b = c) (= 1) (b - a) = a (= b)
(c - b) a b c (c - b) b c(1, 2, 3) (1, 2, 4)
Nicomaque 3 Nicomaque 4
(b - a) = a (b - a) = c
(c - b) c (c - b) a(2, 3, 6) (3, 5, 6)
Nicomaque 5 Nicomaque 6
(b - a) = b (b - a) = c
(c - b) a (c - b) b(2, 4, 5) (1, 4, 6)
Nicomaque 7 Nicomaque 8
(b - a) = a (c - b) = a
(c - a) c (c - a) c(6, 8, 9) (6, 7, 9)
Nicomaque 9 Nicomaque 10
(b - a) = a (c - b) = a
(c - a) b (c - a) b(4, 6, 7) (3, 5, 8)
Théon 11 Théon 12
(b - a) = b (c - b) = b
(c - a) c (c - a) c(0, 1, 2) (3, 4, 6)
CONCLUSIONS :
STATUT DE LA MEDIETE THEON 11
ET STRUCTURE DU SYSTEME DES MEDIETES
La méthode des cribles laisse survivre 12 médiétés, comprenant les 10 médiétés recensées dans la liste de Nicomaque de Gérase, la 11ème médiété recensée notamment dans diverses thèses de mathématique (Théon 12), et enfin une 12e médiété (Théon 11), produisant un compte conforme à la conjecture de Théon de Smyrne.
La médiété Théon 12 ne présente pas de différence significative avec les 10 premières. Cette médiété se note :
(c - b) = b
(c - a) c
Il convient à présent d'examiner le statut, bien particulier quant à lui, de la médiété Théon 11. Commençons par l'examiner.
(b - a) = b
(c - a) c
Cette médiété possède une solution si et seulement si a = 0, et elle alors vraie dans tous les cas, quelles que puissent être les valeurs de b et c ; mais elle s’avère fausse pour toute autre valeur de a.
On a vu qu'un moyen souvent efficace d'extraire le contenu sémantique d'une médiété (comme Nicomaque 2), était de la transformer en un axiome d'existence. On peut donc comprendre cette médiété comme l’affirmation qu’il existe un nombre a tel que (b - a) = b. Autrement dit, il existe un ensemble vide.
Cette soit disant "médiété" n'a pas d’autre signification. En tant que médiété entre trois termes, elle n'énonce rien de plus que l'idée que si a = 0, alors tout nombre b inférieur à c est une "médiété" entre a (zéro) et c ; - le sens du mot médiété se trouvant alors réduit à sa signification la plus vide : que b se situe "n'importe où" entre a et c. La notion de moyenne se trouve diluée dans la généralité la plus abstraite, puisqu'elle se trouve occuper toute la zone comprise entre a (zéro) et c.
Cette médiété est donc particulière par son absence d'intérêt mathématique, autant que par son excessive généralité, qui la dénonce comme une forme "saturée", voire "dégénérée" de la notion de médiété. Mais nous avons vu que le système admettait des gradations de ce genre, en ce sens que la médiété Nicomaque 1 pouvait déjà nous apparaître, par rapport aux autres, comme « à demi-saturée », ou comportant une signification par trop générale (puisque notamment identique aux notions de nombre entier ou d'intervalle régulier). Nous voyons donc qu'il ne s'agit, dans cette médiété Théon 11, que d'un degré supérieur, et du reste ultime, de saturation ou de dégénérescence.
Car ces remarques négatives ne doivent pas masquer l'essentiel :
Les 717 formules ayant été éliminées par la méthode des cribles l'ont été sur la base de défauts sémantiques irrévocables : faux, impossible, doublon d'un autre, etc, défauts dont chacun est une réfutation définitive de sa validité ou de sa signification.
Rien de si négatif ne caractérise la médiété Théon 11.
En effet, ce qu'énonce la médiété Théon 11 est d’une absolue véracité mathématique, à savoir que :
" (S'il existe un ensemble vide)
Il existe un nombre a tel que (b - a ) = b
Et par conséquent tel aussi que :
( b - a ) = b
( c - a ) c
D’autre part, cette médiété ne contrevient à aucun des axiomes du système que nous avons énoncés jusqu'ici.
En effet, ces axiomes n'exigent pas que les éléments de la majeure soient supérieurs à zéro, mais seulement que les différences entre ces éléments le soient. C'est bien le cas dans notre formule, les différences (b - a) et (c - a) sont toutes deux supérieures à zéro.
D'autre part, notre axiome exige également que, dans la mineure, aucun élément ne soit égal à zéro. C'est encore bien le cas de notre formule, puisque le nombre a (égal à zéro) ne figure pas dans la mineure.
Autrement dit, la médiété Théon 11 satisfait bien la forme :
x = a
y b où x, y, a et b sont des nombres positifs supérieurs à zéro.
La médiété Théon 11 est donc libérée de l'escarcelle des cribles logiques au même rang que les onze autres, et ne contrevient à aucun des axiomes énoncés dans le système. C'est à dire que, pour l'éliminer, nous serions obligés d'introduire un axiome et un crible supplémentaire, auxquels contrevienne seule cette médiété ; par exemple : "la majeure non plus ne doit pas contenir d'élément égal à zéro". Un tel décret donnerait du coup l'impression d'être créé "sur mesure" pour éliminer la médiété Théon 11; et son adoption relèverait uniquement, dès lors, d'une situation de choix, dans la définition du système.
Or, il nous faut bien constater que le système lui-même ne nous invite pas à choisir en ce sens.
En effet, que constate-t-on à ce stade dans la structure générale du système?
Si l'on observe l'ensemble des médiétés 7 à 12, on s'aperçoit que la détermination de la médiété Théon 11 (comme celle de n'importe quelle autre médiété de cet ensemble) relève d'un simple exercice de logique amusante. Jugeons plutôt :
( b - a ) = ( a ) ( c - b ) = ( a )
( c - a ) ( c ) ( c - a ) ( c )
( b - a ) = ( a ) ( c - b ) = ( a )
( c - a ) ( b ) ( c - a ) ( b )
( ..... ) = (...) ( c - b ) = ( b )
(.......) (...) ( c - a ) ( c )
Je pense que chacun, en y mettant un peu de coeur, trouvera sans difficulté la médiété n° 11 sans autre étude que l'observation des 5 formules qui l'environnent.
Qu'est-ce que cela signifie pour nous?
Cela signifie que, si la structure des médiétés 1 à 6 était une structure quelque peu capricieuse et asymétrique, dans le cas des médiétés 7 à 12, la structure se caractérise par une parfaite régularité logico-combinatoire. Cette structure se résout, en somme, à une complète relation logique biternaire, développée ici sous la forme topologique :
La conclusion de tout ceci sera donc que le déploiement logique complet du système des médiétés pythagoriciennes conduit à admettre, au titre de médiété n°11, un axiome d'existence du nombre zéro.

 Suivre le flux RSS des articles
Suivre le flux RSS des articles Suivre le flux RSS des commentaires
Suivre le flux RSS des commentaires