L'invention de la théorie musicale

L’INVENTION DE LA THEORIE MUSICALE

Une tradition assez unanime attribue à Pythagore une invention capitale de l’histoire de la pensée, qui est la découverte des rapports mathématiques correspondants aux principaux accords musicaux. L’histoire nous en a été transmise par divers récits, qui sont autant de fictions ou de recréations imaginaires. Ces récits s’efforcent d'apporter une réponse à une énigme historique, qui est  l’ « expérience cruciale » ayant permis cette découverte. La plupart décrivent des expériences dont le principe est scientifiquement correct, mais commettent des erreurs dans l’application du raisonnement. Le fait à retenir pour nous est que la découverte  de Pythagore ait donné lieu, dès la plus haute antiquité, à une multitude de « descriptions d’expériences possibles », qui sont typiques du style et des conventions de la physique moderne.  Hypothèses en forme d'équations ou de généralisations  mathématiques, protocoles d'expériences reproductibles, basés sur la mesure de grandeurs physiques  :  on peut dire que l’invention de Pythagore inclue à titre d'incidente celle de la physique mathématique elle-même. Si Pythagore n'a pas désigné lui même un experimentum crucis, chargé d'en illustrer le principe, c'est en réalité sans importance, parce que son équation constituait en elle-même un programme d’expérimentation évident et multiple : rapport entre la hauteur d’un son et la longueur d’une corde, le poids d’un maillet, etc. Qu'elles aient eu une base réellement expérimentale - car il y en eut -, ou qu'elles fussent seulement théoriques et fictionnelles, comme celle qu'on va lire, les spéculations des pythagoriciens dans les domaines de l'harmonie et de l'acoustique, se signalent par leur direction scientifique, étrangère à l'esprit de l'antiquité : notamment par leur compréhension du phénomène du son, dont la nature vibratoire, voire ondulatoire, était déjà soupçonnée.*

L'un de ces récits, donc, rapporté par plusieurs auteurs antiques et médiévaux, raconte que Pythagore, passant près d’une forge, fut charmé et surpris par les sons de marteaux de différents poids frappant sur une enclume. Il pesa les marteaux et trouva que ceux-ci pesaient respectivement 6, 8, 9 et 12 unités de poids. En rapportant ces nombres à 6, on obtient les fractions suivantes (réduction en facteurs premiers) :

                                      6           8          9         12

                                       1         4/3       3/2       2

Qui sont respectivement l’unisson, la quarte, la quinte et l’octave.

(Précisons que l'expérience ici décrite est incorrecte en ce que, dans le cas de marteaux de différents poids, les rapports corrects ne s'appliquent pas à des nombres entiers, mais aux racines carrées de ces nombres. D'autres récits décrivent des expériences correctes, comme celle prêtée à Hippase sur des disques de bronze de différentes épaisseurs; d'autres encore appliquent le même raisonnement à des cordes de longueurs différentes, ou encore à des vases remplis de différentes quantités d'eau.)

Ce système permet de définir tous les rapports musicaux en n’utilisant que les 4 nombres de la tétractys.

Mais là encore, nous devons remarquer que ces nombres se déduisent de la tétractys d'une manière bien particulière. Non seulement les nombres qui composent les fractions sont les nombres de la tétractys, mais, en disposant les 4 rapports dans cet ordre : 1, 2, 3/2, 4/3, on s’aperçoit que la tétractys est exprimée de manière génétique, puisque ces quatre rapports correspondent, respectivement, au rapport de la première ligne de la tétractys avec elle-même (1 ou 1/1), au rapport de la seconde ligne à la première (2, ou 2/1), au rapport de la troisième ligne à la seconde (3/2), enfin, au rapport de la quatrième ligne à la troisième (4/3).

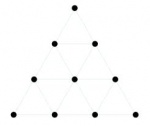
Supersymétrie des accords musicaux et des objets premiers. **

Conclusion : les rapports arithmétiques qui sont ceux des quatre accords fondamentaux de l'harmonie musicale, (unisson, octave, quinte, quarte), correspondent, biunivoquement, aux rapports qu'entretiennent entre eux les quatre objets premiers de la géométrie, (point, segment, triangle équilatéral, tétraèdre), quant au nombre de points qui les composent ou, ce qui revient au même, quant au nombre de sommets qu'ils comportent.

            Unisson              Octave                      Quinte                        Quarte

                  1/1                     2/1                            3/2                                 4/3

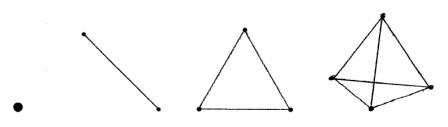
Dans cette application, les objets premiers de la géométrie apparaissent donc, relativement aux accords musicaux, comme des réalités moins primitives, mais en quelque sorte dérivées, puisqu'ils expriment dans leurs rapports mutuels ce que les accords musicaux expriment en eux-mêmes.

L'idée que l'espace et le temps sont des réalités qui ne peuvent se développer que de manière symétrique et coordonnée, est une idée dont on trouve d'autres illustrations dans la littérature pythagoricienne.

Dans les articles suivants, nous verrons que ces rapports musicaux permettent en outre de définir les trois médiétés classiques qui, dans la tradition, jouent le rôle de noyau logique du système complet des 12 médiétés; à savoir la médiété « arithmétique », la médiété « géométrique », et la médiété « harmonique » .

*Contrairement à un préjugé répandu, qui voudrait que la doctrine pythagoricienne ait entretenu une certaine confusion entre les plans mathématique et physique, toutes les expériences que nous rapporte la tradition montrent un étagement correct des niveaux ontologiques : mathématique / physique et hypothèse / expérience. Archytas : "Les sons sont causés par la vibration de l'air. Les sons aigüs correspondent à des mouvements rapides, les sons graves à des mouvements lents." Selon le sentiment de plusieurs historiens de la physique, la première grandeur physique qui soit caractéristique du style et des procédures de la physique moderne, n'est autre que la vitesse archytéenne, qui est, dans toute sa rigueur mathématique, et avec son réel horizon expérimental : la vitesse de vibration de l'air correspondante à la hauteur d'un son. Georges Mourier, historien de la physique ondulatoire, a ainsi montré que la théorie moderne du son se déduisait très naturellement des opérateurs mathématiques mis en oeuvre par Archytas et ses congénères.

** Nous empruntons le terme contemporain de "supersymétrie" pour désigner ce qui est ici, très simplement, une symétrie entre deux symétries, - entre deux séries d'objets dont le principe générateur individuel est déjà une symétrie.