-
Le système des 12 médiétés : démonstration de complétude
LE SYSTEME DES 12 MEDIETES
(démonstration de complétude)
L'objet de cet article est de démontrer que, conformément à la conjecture de Théon de Smyrne, il existe 12 médiétés, mais en outre, qu'il ne peut en exister davantage.
On verra que la résolution du système, ou sa clôture, en onze ou en douze médiétés relève, en ultime instance, d'une situation de choix, qui équivaut à définir le système des médiétés ou bien dans N* (N sauf zéro) ou bien dans N (inclus zéro ou l'ensemble vide). Nous verrons néanmoins que l'adoption de la 12e médiété est recommandée par la symétrie interne du système, au sein duquel cette médiété se réduit à un énoncé qui n'est autre qu'un axiome d'existence du nombre zéro.
Commençons par présenter notre méthode de démonstration.
Dans un premier temps, le problème des médiétés est défini sur un plan strictement logico-formel, qui est celui que nous avons déjà énoncé plus haut :
"Une médiété est une expression à 6 places vides de la forme :
(...) - (...) = (...)
(...) - (...) (...)
dans laquelle les relations arithmétiques sont constantes, et où les six places vides doivent être remplies par les lettres a, b, c, telles que : a < b < c."
Cette définition permet de paramétrer le champ topologique complet du système des médiétés, défini par l'ensemble, intégralement coordonné, de "toutes les formules possibles de ce modèle". Cet ensemble est composé de 36 = 729 éléments.
Lorsqu'on saisit dans cette jungle de formules une formule particulière pour l'examiner dans le détail, il va se produire très souvent (en fait, dans presque tous les cas) que cette formule s'élimine d'elle-même, entraînant dans sa chute d'autres formules du même modèle, par la simple considération de sa signification.
On appelle ici "méthode des cribles" cette méthode de balayage du champ amorphe des formules logoniques, par des moyens sémantiques, issus de l'analyse du sens des propositions. Alors que les planches logoniques I à IX nous donneront de la médiété une image purement formelle et syntaxique, les cribles successifs appliqueront sur ce champ logonique une analyse localisée, formule par formule. Ces cribles considèrent le sens de certaines formules, et, ayant reconnu ce sens comme contraire à la définition d'une médiété, ou bien manifestement faux, ou bien redondant avec une autre formule, éliminent à la suite toutes les formules analogues à la formule incriminée.
La méthode des cribles permet de définir ce qu'est une médiété d'une façon qui est entièrement mathématique, bien que sa forme soit en apparence négative. Les médiétés se trouvent à la fin définies comme les formules qui restent, une fois actionnés l'un après l'autre la totalité des cribles. Néanmoins, cette définition négative peut être "retournée", c'est-à-dire comprise positivement. Une médiété se trouve définie comme une formule n'ayant aucune des propriétés énumérées par les cribles. La définition est mathématiquement complète en ce que :
1. Aucune des 12 médiétés n'a l'une ces propriétés,
2. Seules entre toutes les formules de médiétés, ces 12 ont la propriété de n'avoir aucune de ces propriétés.
Ou bien, synthétiquement : toutes ces formules (de 1 à 12), et seulement elles, ont la propriété de n'avoir aucune de ces propriétés.
Les formules échappant à la succession des cribles se voient ainsi définies comme constituant le système complet des médiétés pythagoriciennes, en tant que système des seules médiétés possibles, résultantes.
Notre programme sera le suivant :
- On introduit un crible initial qu'on appelle le crible zéro, qui permet de passer de 729 formules à 144, à la suite de quoi on expose le principe selon lequel sont construites nos 9 planches logoniques
- On introduit les cribles 1 à 8 en tenant le compte exact des formules éliminées au fur et à mesure.
- On donne à la suite les 9 planches logoniques sur lesquelles s'effectuent ces opérations, planches sur lesquelles sont indiquées, pour chacune des 132 formules éliminées, l'intitulé du crible au nom duquel elle a été supprimée.
- Enfin notre enquête se conclut par quelques remarques finales sur la structure du système des médiétés, ainsi que sur le statut particulier de la médiété Théon 11.
Le crible zéro et la structure des planches logoniques I à IX.
Nous commençons par énoncer une définition de la médiété plus restrictive que celle, purement formulaire, qui nous a servi jusqu'ici, et cette définition nous permettra ensuite d'actionner, non seulement le crible zéro qui nous occupe ici, mais un autre par la suite (le crible 4), en partant du fait qu'un certain nombre de formules ne correspondent pas à cette définition restrictive de la médiété.
Définition :
"Une médiété est une égalité de rapports entre des différences positives et non nulles (majeure), et des nombres positifs et non nuls (mineure). Ou bien, pour parler mathématiquement :
Une médiété est une expression de la forme :
x = a
y b
dans laquelle x, y, a et b sont des nombres positifs supérieurs à zéro.
Dans le contexte qui est celui du pythagorisme, où le zéro, aussi bien que les nombres négatifs, sont réputés n'avoir pas d'existence, une telle limitation, - qui est naturellement respectée aussi bien dans les 10 médiétés de Nicomaque que dans la 11ème qui lui a été ajoutée par les commentateurs modernes, - une telle restriction n'apparaîtra pas abusive, mais bien plutôt, elle nous semblera pointer une propriété implicite de ce que nous comprenons, dans ces 11 exemples, comme étant une médiété.
Cette nouvelle définition permet de supprimer un grand nombre de formules, et notamment toutes celles (crible zéro) qui, dans leur partie majeure, contiennent une différence de type (a - b) ou encore (b - c), autrement dit une différence où le terme le plus petit précède le plus grand, et dont le résultat est, de ce fait, négatif. Notre définition de la médiété n'admettant que des différences positives, toutes les formules de ce type ne sont pas autorisées.
Il nous faut ici définir avec précision les limites exactes introduites par cet axiome. Notre définition n'oblige pas par exemple les éléments (a, b ou c) intervenant dans la majeure à être non nuls, mais seulement les différences entre ces éléments. Par contre, du côté de la mineure, les éléments doivent être non nuls, c'est à-dire qu'un terme (a, b ou c) figurant dans la mineure, ne peut pas être égal à zéro. Cette précision aura toute son importance lorsque nous aurons à examiner le statut particulier de la médiété Théon 11.
Examinons maintenant plus en détail la situation combinatoire - ou logonique - déterminée par l'actionnement du crible zéro.
Alors qu'auparavant nous avions, pour chaque case du diagramme, trois solutions possibles, (a, b ou c), la somme de ces solutions étant dès lors égale à 36 = 729 formules, ne sont plus permises désormais, dans chacune des cases du logon à 6 places, que les solutions suivantes :
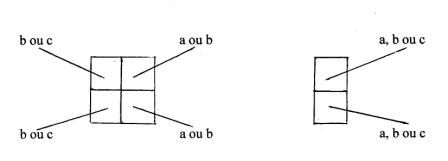
Soit en tout : 2 x 2 x 2 x 2 (= 16 ) x 3 x 3 = 144 formules seulement.
Cette analyse nous permet d'expliciter la structure de nos 9 planches logoniques.
La formule majeure constitue un système combinatoire autonome comportant 16 solutions seulement. Ces 16 solutions sont développées identiquement sur chacune des planches de notre logothèque : ce qui signifie que nos 9 planches sont identiques pour ce qui est de la formule majeure et ne différent entre elles que par la mineure. Ces neuf planches correspondent tout simplement aux 9 solutions possibles (3x3) pour le "remplissage" de la mineure soit : (a/a, b/b, c/c, a/b, b/a, a/c, c/a, b/c, c/b).
Ce qui nous donne bien, au total 16 x 9 = 144 formules
Ces précisions nous permettent en outre d'attribuer à chaque formule un numéro d'ordre à deux coordonnées, de type (II, 4), dans lequel le chiffre romain indique le numéro de la planche (qui permet donc de retrouver sa formule droite ou mineure), et le chiffre arabe son rang dans le développement de 1 à 16 de la partie majeure.
C'est donc sur ce champ logonique réduit que vont désormais s'appliquer les 8 cribles successifs énumérés ci-après.
Sur les 729 formules dont nous disposions au départ, le crible zéro a supprimé toutes les formules contenant une différence négative, de forme (a - b), (a - c) ou (b - c), mais aussi les deux tiers des formules contenant une différence nulle (les formules en (a - a) et (c - c)). Seules les différences nulles de la forme (b - b) ont résisté au crible zéro, puisque notre diagramme prend en compte uniquement les solutions possibles pour chacune des cases du tableau, sans préjuger de ce qui figure sur une autre case du même tableau; or, la lettre b est la seule à être possible sur chacune des 6 cases du diagramme, contrairement aux lettres a et c. La suppression des formules contenant l'expression (b - b) devra donc faire l'objet d'un crible spécial ultérieurement (crible 4).
Crible 1 : « Ne contient pas trois lettres »
Une médiété est un rapport entre trois termes (a, b, c)
Sur nos 144 formules, le critère : "cette formule ne contient pas trois lettres, est n'est donc qu'une relation entre - au maximum - deux éléments" - ce critère permet d'éliminer 34 formules.
Restent 144 - 34 = 110 formules.
Crible 2 : « Formule miroir »
On peut éliminer toutes les formules dans les quelles le haut et le bas (de la formule) sont identiques.
Prenons par exemple la formule :
b a c
b a c, qui se lit :
(b - a) = c
(b - a) c
Le sens de cette formule n'est qu'une pure évidence mathématique qui énonce :
x/x = y/y (=1)
En tout état de cause, cette formule n'énonce pas une relation déterminée entre trois termes réciproquement définis, mais une évidence mathématique valable indistinctement pour tout nombre n.
Ce critère élimine quatre nouvelles formules. Restent 110 - 4 = 106 formules.
Crible 3 : « Image de (..., ...) »
On peut supprimer toutes les formules qui peuvent être obtenues à partir d'une autre formule, en inversant le haut et le bas.
Par exemple la formule :
b a c
c b a
Cette formule peut-être obtenue à partir de la formule :
c b a
b a c en inversant les lignes du haut et du bas.
En réalité, ces deux formules ne sont pas deux formules différentes, mais l'une n'est qu'une conséquence mathématique triviale de l'autre, en vertu de l'évidence selon laquelle :
si (a/x) = (b/y) alors (x/a) = (y/b)
Autrement dit, nous n'avons pas affaire à deux formules différentes, mais à deux expressions équivalantes de la même formule. Pour cette raison, l'une ou l'autre de ces formules peut indifférement être éliminée, et l'autre conservée comme un représentant valable de la formule considérée. Ici, on choisit arbitrairement de conserver la première qui apparaît dans notre liste.
Le critère "Cette formule est l'image de la formule (..., ...) permet à lui seul d'éliminer la moitié des formules subsistantes, ce qui laisse subsister 106/2 = 53 formules.
Notons en particulier que trois planches entières peuvent être rayées d'un seul trait de plume. En effet, la planche 5, par exemple, étant tout simplement l'image de la planche 4, peut être supprimée intégralement. Même chose pour les planches 7 et 9, qui sont respectivement les images des planches 6 et 8.
Crible 4 : « Contient une différence nulle »
Selon notre définition initiale d'une médiété, les différences entre deux termes qui figurent dans la majeure doivent être des valeurs positives et non nulles. Cette restriction a déjà permis d'éliminer, à l'occasion du crible zéro, toutes les formules dans lesquelles figurait une différence négative, ainsi que les formules contenant une différence nulle de la forme (a - a) ou (c - c).
A présent, la même restriction nous permet d'éliminer toutes les formules subsistantes où figure une différence nulle, de la forme (b - b), - formules qui, pas plus que les précédentes, ne sont permises par notre définition.
Le critère "Cette formule contient une différence nulle" permet d'éliminer 20 nouvelles formules, et il nous reste à ce stade 53 - 20 = 33 formules.
Crible 5 : « Faux 1 »
Examinons maintenant la formule Nicomaque 1, qui nous est familière :
( c - b ) = a ( = 1 )
( b - a ) a
Cette formule implique que ( c - b ) = ( b - a )
De la même manière, toutes les formules qui ont pour mineure une sous-formule du type ( x/x ) (= 1), impliquent que, dans la majeure, la différence du haut soit égale à la différence du bas.
Cette analyse permet dès lors d'éliminer un certain nombre de formules comme mathématiquement fausses.
En effet, toutes les formules dans lesquelles on a à la fois, dans la mineure, une fraction de type ( x/x ), et, dans la majeure, deux lettres identiques se situant sur une même verticale, toutes ces formules sont, de toute évidence, mathématiquement fausses.
Prenons par exemple la formule :
( c - a ) = a
( b - a ) a
Cette formule contient, dans sa mineure, une expression de la forme (x/x) (=1), et, dans sa majeure, deux lettres identiques sur une même verticale (a/a). Cela signifie que, pour que cette formule soit vraie, il faudrait tout simplement que b = c, ce qui est interdit par définition, puisqu'on a toujours b < c.
Ce critère "Faux 1" permet d'éliminer 6 nouvelles formules, et il nous reste à ce stade 33 - 6 = 27 formules.
Crible 6 : « Faux 2 »
Une autre famille de formules peuvent être reconnues fausses par hypothèse, les formules où l'on a en face d'une mineure de type (x/y) une majeure de type : (o - g) / (o - g)
soit une formule de la forme :
(o - g) = x
(o - g) y
Dont un exemplaire pris au hasard est la formule :
(c - a) = a
(c - a) b
Une telle formule est évidemment fausse. En effet, pour que cette formule soit vraie, il faudrait que a = b, ce qui est impossible, puisqu'on a par définition : a < b.
Ce critère élimine à son tour 6 nouvelles formules, et il nous reste à ce stade 27 - 6 = 21 formules.
Crible 7 : « Doublon de Nicomaque 1 ou 2 »
Notre connaissance particulière des médiétés Nicomaque 1 et Nicomaque 2 nous suggère ici l'idée d'un crible supplémentaire.
Nous savons qu'entre toutes les médiétés connues, la médiété Nicomaque 1 est la seule à comporter 3 fractions dans sa partie mineure, tandis que la médiété Nicomaque 2 est la seule à compter 2 fractions dans sa partie mineure, alors que toutes les autres médiétés connues ne comptent, dans leur partie mineure, qu'une seule et unique fraction.
Nous avons donc d'ores et déjà connaissance de trois formules qui ne sont pas des médiétés autonomes mais, pour les deux premières, ne sont autres que la médiété Nicomaque 1, bis et ter, et pour la troisième, la médiété Nicomaque 2 bis. Nous savons en effet que ces doublons particuliers ne correspondent pas à des médiétés différentes, mais à de simples variantes des médiétés susdites, ayant les mêmes solutions.
Ce critère nous permet donc d'éliminer 3 nouvelles formules.
Et il nous reste : 21 - 3 = 18 formules.
Crible 8 : « Faux 3 »
Examinons la formule :
( c - a ) = a
( c - b ) b
Par hypothèse ( c - a ) > ( c - b ) puisqu'on a : a < b.
Ce qui fait que nous avons là une formule qui énonce elle même les rapports suivants entre ses quantités :
(plus grand que dessous) = (plus petit que dessous)
(plus petit que dessus) (plus grand que dessus)
Cette formule est mathématiquement absurde, car le rapport d'un plus grand nombre sur un plus petit ne peut pas être égal à celui d'un plus petit sur un plus grand, pour la raison, tout simplement, que le premier est nécessairement supérieur à 1, tandis que le second est nécessairement inférieur à 1.
Ce critère permet d'éliminer 6 nouvelles formules, et les 12 formules qui nous restent constituent le système des 12 médiétés pythagoriciennes. CQFD.
Notre démonstration établit qu'il ne peut exister plus de 12 médiétés pythagoriciennes, puisque toute autre formule que ces 12 appartient à l'une ou l'autre des catégories de formules qui, pour ainsi dire, énoncent elles-mêmes qu'elles ne sont pas des médiétés, et ont pu sur cette base être éliminées sur des critères purement sémantiques. En outre, nous devons être bien convaincus d'avoir, par la méthode des cribles, parcouru la totalité du champ logique dans lequel s'inscrivent les médiétés; c'est-à-dire que nous savons réellement ce qu'énonce individuellement chacune des 717 formules éliminées depuis la mise en oeuvre du crible zéro.