LA THEORIE DU GNOMON

 

 

 

  

GNOMON D’UN POLYGONE REGULIER

 

  

La loi du gnomon

 

Le gnomon du carré est égal au gnomon du triangle équilatéral, égale 3.

 

G (c) = G (t e) = 3

 

Définition : On appelle gnomon d’un polygone régulier, la plus petite quantité du même polygone, que l’on doive lui ajouter, pour qu’un polygone semblable soit reconstitué.

A tout carré, il faut ajouter 3 carrés identiques au premier, pour qu’un carré soit reconstitué.

A tout triangle équilatéral, il faut ajouter trois triangles équilatéraux identiques au premier, pour qu’un triangle équilatéral soit reconstitué. 

   

Pour chacun de ces polygones, on a :

G(g) = 3g

"Le gnomon de l'objet g est égal à 3g"

Ou encore : pour chacun de ces polygones, le rapport de l'objet g à son gnomon est de 1/3.

Ainsi, de la même manière qu'il faut compter jusqu'à quatre, qu'il faut quatre "pas" pour avoir la base arithmétique (10), pour avoir les dimensions de l'espace et les objets premiers de la géométrie, mais aussi les rapports musicaux fondamentaux, de même, il faut quatre pas pour avoir la structure du gnomon.

Notons que le triangle gnomonique de rang 2 (c'est à dire de "côté" 2), ci-dessus, est matériellement identique à un tétraèdre déplié. Or on a vu qu'il suffisait de quatre "pas" (quatre points) pour construire le tétraèdre, et ces quatre points de référence peuvent être aussi bien les sommets du tétraèdre, que les centres de ses quatre faces, repérés ci-dessus par des points, et reliés entre eux par un trépied. Le tétraèdre, qui est le plus simple des polyèdres, et le triangle gnomonique de rang 2, qui est le premier et le plus simple des gnomons, doivent donc être compris comme deux modalités contigües, bien que mathématiquement distinctes, de la "clôture à quatre" : l'une géométrique, l'autre, comme on le verra dans nos deux derniers articles, de nature essentiellement logique.

 

  

  

Loi de progression impaire et infinie des gnomons successifs du triangle et du carré

 

Si l’on ajoute à un triangle équilatéral ou à un carré une quantité indéfinie d’objets identiques au premier, la figure initiale se reconstitue à l’infini au moyen de gnomons successifs, dont les valeurs sont celles des entiers impairs supérieurs à 1.

 

 

 

 

La progression des gnomons successifs du triangle équilatéral et du carré, n’est autre que la progression infinie des nombres entiers impairs supérieurs à 1. Ou encore : l’ensemble des gnomons du triangle équilatéral et du carré, correspond à l’ensemble des entiers impairs supérieurs à 1. 

Dans l'esprit de la mathématique moderne, il est possible de considérer l'unité, appelée aussi graine du gnomon, comme "gnomon de rang zéro", ou gnomon nul, et dans ce cas on obtient :

 

G (te) = G (c) = I

 

L'ensemble des gnomons du triangle équilatéral, est égal à l'ensemble des gnomons du carré, est égal à l'ensemble des entiers impairs.

 

Bien qu'on puisse en être surpris, cette loi, qui est l'une des plus importantes de la mathématique pythagoricienne, ne figure, à notre connaissance, dans aucun livre de mathématique ancien ou moderne.

 

 

 

Loi de croissance arithmétique et infinie des côtés des carrés et triangles gnomoniques

 

On appelle polygone gnomonique de rang n, tout carré ou triangle reconstitué, formé d’un carré ou d’un triangle originaire, appelé graine, et d’une quantité quelconque - inclue zéro - de ses gnomons successifs.

Le polygone gnomonique de rang 1 n'est autre la graine (gnomon zéro).

Les objets suivants sont tous des carrés ou des triangles gnomoniques.

 

 

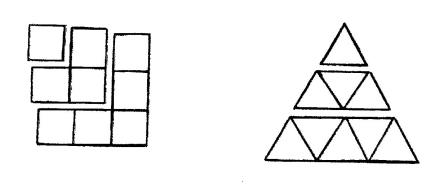
La croissance des côtés des polygones gnomoniques successifs, formés à partir d’un polygone quelconque (graine), de valeur 1, n’est autre que la croissance des nombres entiers naturels.

 

  

 

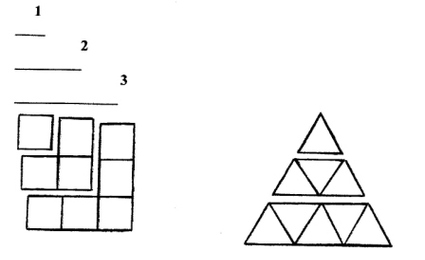
Si la graine, triangle ou carré, mesure 1 cm, alors, les triangles ou carrés gnomoniques de rang (2, 3, 4...) formés à partir de cette graine mesureront respectivement (2, 3, 4…) cm.

  

  

 

Loi de progression carrée des aires des polygones gnomoniques

     

Les valeurs des aires des polygones gnomoniques successifs sont égales aux carrés des nombres entiers naturels.

 

Par application directe de ce que nous venons d’exposer sur les côtés des polygones gnomoniques, on constate que la croissance de la surface, de l’aire, des polygones gnomoniques successifs, n’est autre que celle des carrés des nombres entiers naturels. 

 S ( PG ) = n²

Où n est le nombre entier correspondant au côté du polygone. 

Si nous avons adopté la convention d’appeler « carré » la puissance 2 d’un nombre, son produit par lui-même, c’est en illustration directe de la loi du gnomon, qui veut que le carré se reconstitue selon un rythme qui n’est autre que celui des « puissances 2 » du nombre entier naturel. 

On peut penser que cet usage, conservé jusqu'à nous par la tradition mathématique, est un héritage direct de la spéculation pythagoricienne sur le gnomon. Néanmoins, en toute rigueur, nous devons remarquer que rien n’empêche d’appeler « triangles » les nombres que nous appelons « carrés », puisqu’on a vu que le triangle gnomonique se reconstituait selon les mêmes valeurs numériques que le carré. La préférence donnée au carré pour symboliser la puissance 2 du nombre, s'explique uniquement par le fait que, pour le carré, la correspondance entre nombre et figure peut se poursuivre dans la troisième dimension (nombres cubiques), comme on le verra dans le prochain article, ce qui n'est pas le cas pour le triangle. 

 

   

 

Complétude du système

 

Un polygone régulier du plan est une figure fermée du plan dont tous les côtés sont égaux.

Le triangle équilatéral est le polygone régulier qui possède le plus petit nombre de côtés (puisque avec deux segments, on ne peut former une figure fermée.) A chaque nombre entier supérieur à 2, correspond donc un polygone régulier.

 

Dans la série infinie des polygones réguliers, seuls le triangle équilatéral et le carré possèdent un gnomon.

  

Démonstration.   

En premier lieu, pour qu’un polygone régulier puisse avoir un gnomon, il est nécessaire que ce polygone soit une solution de pavage continu du plan. En effet, les polygones gnomoniques, qui sont simplement des polygones formés de parties semblables à eux-mêmes, sont des figures complètes et continues du plan, sans reste ni vide. Or seuls trois polygones réguliers sont des solutions de pavage continu du plan : le triangle équilatéral, le carré et l’hexagone. (La démonstration de cela est du domaine public). L’hexagone ne possède pas de gnomon, car il est impossible de construire un grand hexagone au moyen d’hexagones plus petits. Donc, seuls le triangle équilatéral et le carré possèdent un gnomon.

 

  

 

Gnomons et symétrie

  

A. Le carré

 

Si l’on examine un carré gnomonique de rang quelconque, on constate que les centres des carrés élémentaires forment une constellation de points, distribués dans le plan en symétrie orthogonale.

  

 

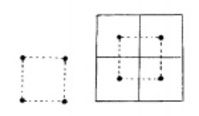
Notons que cette symétrie est la même que celle qui existe entre les points qui sont les sommets des carrés atomiques ou élémentaires.

 

 

B. Le triangle

 

Si l’on examine maintenant un triangle gnomonique de rang quelconque, on constate que les centres des triangles élémentaires se distribuent selon une symétrie dihexagonale.

  

  

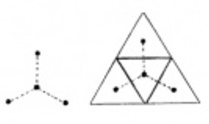
Cette symétrie est différente de celle qui existe entre les points qui sont les sommets des triangles élémentaires, et qui est une symétrie hexagonale simple. Une symétrie dihexagonale est un système plus complexe qu’une symétrie simplement hexagonale, puisqu’elle est constituée de deux réseaux hexagonaux entrelacés, comme on le voit ci-dessous.

 

   

Pour caractériser la différence entre les deux systèmes, on peut remarquer que les noeuds d’un réseau hexagonal sont reliés par des triangles, alors que ceux d’un réseau dihexagonal sont reliés par des trépieds. 

 

     

    Réseau hexagonal      Réseau dihexagonal     Triangle gnomonique

         (triangles)                      (trépieds)

  

Dans le schéma ci-dessus à droite, on voit bien que si les sommets d’un triangle gnomonique appartiennent à la première sorte de symétrie, les centres du même triangle appartiennent, eux, à la seconde.

 

 

 

Remarque

 

Dans la théorie pseudo-pythagoricienne des "nombres figurés", les « nombres carrés » (engendrés en comptant les points d’une constellation orthogonale) sont comparés aux « nombres triangles » (comptés sur une constellation hexagonale), et leur sont opposés, comme formant deux familles différentes. Mais dans la théorie mathématique rigoureuse du gnomon, une telle façon de procéder n’a pas de sens, car les nombres auxquels doivent être comparés, en toute rigueur, les nombres carrés, ce ne sont pas les nombres triangulaires, mais les nombres trépieds, dénombrés sur une constellation di-hexagonale. Et ce que l’on obtient alors, ce n’est pas une « opposition » entre deux familles, mais une équation :

 

 Le nombre carré est égal au nombre trépied.

 

N ( C ) = N ( T )

  

En appelant ici "nombre trépied" le nombre de points que l'on obtient en empilant progressivement des trépieds les uns sur les autres, selon une progression arithmétique, ou "pyramidale", analogue à celle de la tétractys.

  

  

  

Loi de transformation du triangle en carré

 

Il est possible de donner de cela une démonstration géométrique.

Dans tout triangle gnomonique de rang supérieur à 1, on remarque l’alternance entre des triangles orientés « pointe en haut » (en gris), et d’autres, en nombre inférieur, orientés « pointe en bas » (en blanc).

  

En faisant subir à ces triangles blancs une rotation de 180 degrés sur la base horizontale du triangle gnomonique, on obtient un parallélogramme qui, moyennant un simple changement de paramètre angulaire (passage du mode di-hexagonal au mode orthogonal) s'avère être un carré gnomonique.

 

                                                                            

Rotation des triangles "pointe en bas"        Modification du paramètre angulaire

de 180 °                                                                             (de 60 ° à 90 °)

 

A n’importe quelle échelle de son développement, le triangle gnomonique se transforme en carré gnomonique au moyen de ces deux opérations : rotation de 180 degrés des triangles « pointe en bas », et variation de 30 degrés du paramètre angulaire.

 

           

 

   

GNOMON D’UN POLYEDRE REGULIER

 

  

  

Les polyèdres réguliers

 

On appelle ici polyèdres réguliers (ou solides réguliers), suivant l'usage commun, la seule famille étroite des polyèdres réguliers convexes, appelés aussi solides pythagoriciens, ou, abusivement, platoniciens. Les polyèdres réguliers convexes sont au nombre de 5, tandis qu'avec les concaves, la famille s'élargit à 9.

Les polyèdres réguliers sont à la famille des polyèdres, ce que les polygones réguliers sont à la famille des polygones. En pythagorisme, ils appartiennent à la catégorie des objets géométriques "premiers en naissance". De même que les polygones réguliers (dimension 3) sont construits avec le matériel le plus simple que l'on puisse trouver dans la dimension inférieure (des segments de longueur identique), de même, les polyèdres réguliers (dimension 4) sont construits avec les objets les plus simples de la dimension inférieure : des polygones réguliers identiques. 

  

  

                              Tétraèdre                                              Cube                     

                     Octaèdre                  Dodécaèdre                  Icosaèdre 

 

 

Leurs faces sont toutes des polygones réguliers identiques, leurs angles et leurs sommets sont tous identiques. Mathématiquement, ils sont absolument symétriques en chacune de leurs faces, de leurs angles et de leurs sommets (symétrie de rotation).

Les propriétés principales de ces figures étant bien connues et documentées (les plus importantes étant, outre la démonstration qu'il n'en existe que cinq, la dualité et la loi d'Euler), on se dispensera de les rappeler ici, pour nous limiter à ce qui concerne la théorie du gnomon.

  

  *  

             

Si l’on applique aux polyèdres une méthode de construction analogue à celle employée pour les polygones, alors :

 

Seul le cube possède un gnomon tridimensionnel.

 

Dans un polygone gnomonique, triangle ou carré, on remarque cette propriété particulière que la graine (la forme géométrique à reconstituer, considérée comme l’origine de la série des gnomons) et l’atome (l’élément unique, ou « brique topologique » servant à la construction des gnomons) sont identiques.

Dans le cas des polyèdres réguliers, cette propriété (identité de la graine et de l’atome) est observée pour le cube, et pour le cube seulement.

Avec plusieurs petits cubes de même taille, on peut en effet construire un cube plus grand, mais la chose s’avère impossible pour chacun des 4 autres polyèdres réguliers. Avec plusieurs petits tétraèdres, il est impossible de construire un plus grand tétraèdre, idem pour l’octaèdre, le dodécaèdre et l’icosaèdre.

 

 

 

Le gnomon facial

 

Ce qui suit n’est donc plus un raisonnement portant sur la constitution interne de l’objet, mais uniquement sur sa structure et son aspect externe, autrement dit sur sa face.

On appelle maintenant gnomon facial d’un polyèdre, le solide qui, ajouté à ce polyèdre, permet de reconstituer un polyèdre semblable, dont la face est un polygone gnomonique de rang supérieur.

En suivant cette définition, 4 des 5 polyèdres réguliers possèdent un gnomon facial. 

Simplement, dans 3 de ceux-ci, la graine (la forme à reproduire) n’est pas identique à l’atome (la brique de construction), et l’atome n’est pas unique (deux atomes pour le tétraèdre et l’octaèdre, trois atomes pour l’icosaèdre).

 

 

 

Complétude du système

  

Parmi les 5 polyèdres réguliers, l’un d’entre eux, le dodécaèdre, ne peut pas posséder de gnomon facial.

 

Démonstration.

La démonstration s’appuie sur celle que nous avons donnée plus haut, montrant que, parmi les polygones réguliers, seuls le triangle équilatéral et le carré possèdent un gnomon. 

En effet, d’après cette limitation, pour qu’un  polyèdre puisse avoir un gnomon facial, il faut de toute nécessité que sa face soit ou bien un triangle, ou bien un carré. La face du dodécaèdre étant un pentagone, celui-ci ne peut avoir de gnomon facial, puisque le pentagone n’est pas une solution de pavage continu du plan. 

Quant aux quatre autres polyèdres réguliers, nous allons voir que chacun d’eux possède effectivement un gnomon facial.

A la fin de cet article, un tableau récapitule les valeurs des 4 premiers gnomons de ces polyèdres.

  

 

 

Gnomon du cube

 

Le cube est, comme on l’a vu, le seul polyèdre régulier dont le gnomon n’est pas seulement un gnomon facial, mais un gnomon au sens interne et constitutif du terme, puisque, dans celui-ci, la graine, la forme à reproduire, est identique à l’atome, pièce unique servant à sa construction.

Les premiers gnomons du cube correspondent aux nombres : 7, 19, 37, 61, etc,

et la règle qui permet de les trouver est la suivante :

  

G (c) = 1 (+ 6), (+12), (+18), (+24), (...), (+ 6 x n)

  

Mais pour comprendre cette série, il est encore plus simple de considérer les nombres correspondants à chacun des cubes gnomoniques reconstitués. En effet, ces nombres sont tout simplement les cubes des nombres entiers naturels.

1, 8, 27, 64, 125, ...,  n³

 

Nous voyons ainsi que la théorie « classique » des nombres cubiques, telle qu’elle est passée sans altération de la tradition pythagoricienne jusqu'à nous, est elle aussi en accord avec la définition mathématique rigoureuse du gnomon, contrairement à la théorie malencontreuse des nombres « figurés », qui en est une tentative d'extension illégitime. Dans cette théorie classique, les nombres appelés cubiques sont les nombres correspondants à chacun des cubes gnomoniques reconstitués, chacune des phases de « réalisation » ou de complétude du cube, incluant la graine, l’unité, dans la série. Si nous avons adopté la convention de nommer « cube » la puissance 3 d’un nombre, de la même manière qu’on appelle « carrés » les nombres correspondants à la croissance de la surface du carré gnomonique, c’est donc là aussi par référence à une théorie mathématique exacte du gnomon.

 

Le fameux « Rubix-Cube » peut être pris comme un exemple valable de cube gnomonique (gnomon d'ordre 2). S’il était réellement constitué uniquement de petits cubes, il serait constitué de 27 éléments : 3³.

 

 

  

  

Gnomon du tétraèdre

 

Pour chacun de nos gnomons futurs, la graine est coloriée en rouge, l’atome-octaèdre en blanc et l’atome-tétraèdre en gris.

 

       

 

                 Tétraèdre                                               Gnomon du tétraèdre

 

   

On peut vérifier visuellement que la face du grand tétraèdre (triangle gnomonique de rang 2) est bien un gnomon polygonal de celle du petit tétraèdre – en rouge – qui est sa graine. 

 

Le gnomon (facial) du tétraèdre est un solide en forme de pyramide (tétraédrique) tronquée, composé de 4 éléments : 1 octaèdre et 3 tétraèdres. La série infinie des gnomons suivants se développe ainsi : 

 

 G (t) = (1/3); (3/6); (6/10); (10/15); (15/21); (21/28); ...; (a/b)

 

On appelle « b » la valeur de droite de chaque fraction, correspondant aux atomes-tétraèdres. On voit que les valeurs successives de b sont engendrés à partir de la première (3), par les opérations :

 

b = 3; +3; +4; +5; +6; …

 

Notons que la graine du gnomon peut être intégrée dans la série des « b » sans déroger à la règle + n (avec n supérieur à 1) qui est celle de la série, puisqu’on a :

 

1 (graine) + 2 (premier gnomon), +3, +4, etc

 

Quant à la valeur « a », valeur de gauche de chaque fraction, correspondant aux atomes-octaèdres, elle n’est autre, à chaque fois, que la valeur « b » de la fraction précédente (y compris la première « 1 » qui correspond à la valeur b du rang précédent, qui est le rang de la graine). La série des valeurs « a » est identique à la série des « b », mais avec un temps de retard.

 

A présent, il est particulièrement intéressant d’opérer la simplification de ces fractions.

 

On observe ceci :

 

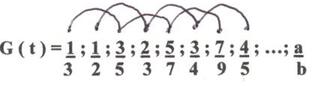
En suivant le développement de la valeur "a" selon deux chaînes alternées, on s’aperçoit que ces deux chaînes nous présentent, l’une, la série des nombres impairs et, l’autre, la série des nombres entiers.  

a = 1, …, 3, …, 5, …, (série des nombres impairs)

a =…, 1, …, 2, …, 3, … (série des nombres entiers)

 

Le constat est le même pour la valeur b, mais avec un rang de décalage : 

b = 3, …, 5, …, 7, … (série des nombres impairs supérieurs à 1) 

b =…, 2, …, 3, …, 4, … (série des nombres entiers supérieurs à 1) 

  

 En résumé, dans cette alternance de fractions, la première chaîne : 

 G (t) = (1/3); (...); (3/5); (...); (5/7): ...

exprime le rapport de chaque nombre impair à son successeur. 

La deuxième chaîne :

 G (t) = (...); (1/2); (...); (2/3); (...); (3/4); ... 

exprime le rapport de chaque nombre entier à son successeur.

 

 

 

Gnomon de l’octaèdre

 

Le gnomon de l’octaèdre est constitué des mêmes éléments atomiques que celui du tétraèdre : tétraèdres et octaèdres. Seule leur proportion change donc.

 

    

              Octaèdre                                                  Gnomon de l’octaèdre

 

La face du grand octaèdre est bien un gnomon polygonal de celle du petit octaèdre (graine).

Le gnomon immédiat de l’octaèdre est constitué de 5 octaèdres et 8 tétraèdres.           

Les gnomons ultérieurs se développent de la façon suivante :

 

 G (o) = (5/8); (13/16); (25/28); (41/44); (61/64); ...; (a/b)

 

On remarque que la valeur de a évolue selon la règle suivante :

 

a = 5 ; +8 ; +12 ; +16 ; +20 ; …

 

Notons que, là aussi, la graine du gnomon, constituée d’1 octaèdre, peut être comprise dans la série des valeurs « a » à titre de terme originaire, sans faire exception à la règle (+ 4 x n) qui régit la suite des gnomons.

En effet :

 

1 (graine) +4 = ; 5 (premier gnomon); +8; +12; …

 

Quant à la valeur b, on remarque qu’elle se déduit directement de a, puisque l’on a :

b = a + 3

 

 

 

Gnomon de l’icosaèdre

 

Le gnomon de l’icosaèdre se construit au moyen des deux mêmes éléments atomiques que les gnomons du tétraèdre et de l’octaèdre : des octaèdres (a) et des tétraèdres (b); cependant le système inclue un élément atomique de plus (d) qui est la propre graine de l’icosaèdre.

Les valeurs de ce gnomon évoluent beaucoup plus rapidement que celles des précédents, puisque le premier gnomon de l’icosaèdre est déjà composé de 20 octaèdres et 60 tétraèdres.

Voici la façon dont ce solide se construit.

Sur chacune des 20 faces de l’icosaèdre (en rouge), on « colle » un octaèdre. La figure qui apparaît ensuite est celle d’un ballon sur lequel 12 cratères ou cupules se présentent, correspondants aux 12 sommets de l’icosaèdre primitif. Dans chacune de ces 12 cupules se logent 5 tétraèdres, soit 12 x 5 = 60 tétraèdres en tout.

Comme il était fastidieux de réaliser en papier les 81 solides nécessaires à cette construction, on n’en a réalisé ici qu’une partie, suffisante pour en détailler les trois étapes.  

 

            

Gnomon de l’icosaèdre (construction)      Cupule remplie de 5 tétraèdres (en haut)

                                                                    et face complète du grand icosaèdre (en bas)

 

En dépit de ses dimensions imposantes, ce gnomon est bien un gnomon facial du premier rang, (dont la face est un triangle gnomonique de rang 2); de sorte que le rapport 20/60 est l’équivalent exact, pour l’icosaèdre, des rapports 1/3 et 5/8 enregistrés pour les polyèdres précédents.

Quant au calcul des valeurs suivantes de l’icosaèdre, il ne pose guère de difficulté, puisqu’on remarque immédiatement que ces valeurs sont égales à 20 fois celles du tétraèdre. Déroulons l’une au dessus de l’autre les deux séries de gnomons :

 

 G (t) = (1/3); (3/6); (6/10); (10/15); (15/21); ...; (a/b) 

 

G (i) = (20/60); (60/120); (120/200); (200/300); (300/420); ...; (a/b)

   

Les valeurs du gnomon de l’icosaèdre (en bas) se déduisent de celles du tétraèdre (en haut), en multipliant celles-ci par 20. 

Autrement dit, on a :

 

G ( i ) = G ( t ) x 20

 

  

 

Tableau récapitulatif des valeurs des 4 premiers gnomons des polyèdres réguliers

 

Le tableau qui suit indique, pour chacun des polyèdres gnomoniques, les valeurs de ses quatre premiers gnomons.

 

	graine	Gnomon 1	Gnomon 2	Gnomon 3	Gnomon 4
cube	1c	7c	19c	37c	61c
Total PG	1c	8c	27c	64c	125c
tétraèdre	1b	1a, 3b	3a, 6b	6a, 10b	10a, 15b
Total PG	1b	1a, 4b	4a, 10b	10a, 20b	20a, 35b
octaèdre	1a	5a, 8b	13a, 16b	25a, 28b	41a, 44b
Total PG	1a	6a, 8b	19a, 24b	44a, 52b	85a, 96b
icosaèdre	1d	20a, 60b	60a, 120b	120a, 200b	200a, 300b
Total PG	1d	1d, 20a, 60b	1d, 80a, 180b	1d,200a, 380b	1d,400a, 680b

 

a : octaèdre

b : tétraèdre

c : cube

d : icosaèdre

PG : polyèdre gnomonique

 

 

 

 

 

LES DEFINITIONS VAGUES DU GNOMON

 

 

  

 A. Le gnomon géométrique

 

Dans ses Eléments de géométrie, Euclide emploie le terme "gnomon" pour désigner une relation qui est exclusivement géométrique, et non arithmétique, et qui est celle, absolument générale, qu'entretiennent entre eux deux polygones semblables, mais de dimensions différentes, quelles que puissent être ces dimensions. En effet, en prenant, par exemple, deux carrés de dimensions différentes, (ces dimensions étant absolument quelconques), et en les coordonnant par un de leurs angles, on fait apparaître une figure en forme d'équerre, définie par la différence entre les deux carrés. Euclide appelle donc "gnomon" la simple différence entre ces deux carrés, autrement dit la figure qu'il faut ajouter au plus petit pour obtenir le plus grand.

  

  

Défini ainsi, le gnomon revêt une signification qui est donc, dans son contenu, un simple corrélat de la notion commune de croissance géométrique, - une signification qui est donc à la fois très générale, mais singulièrement appauvrie sur le plan des principes. 

En effet, dans cette définition, de nombreux éléments appartenant à la théorie exacte du gnomon sont laissés de côté. Notamment, la notion quantifiée de gnomon minimum d'un polygone; ainsi que de multiples notions logiques, telles que les notions d'espace logique, de système de différences combinatoires, notions qui, comme nous le montrerons dans la dernière partie de cet exposé, découlent uniquement de la théorie exacte du gnomon.

Le gnomon, rappelons-le, est une structure logique, qui en tant que telle, n'appartient en propre ni à l'arithmétique, ni à la géométrie, mais à leur interface, à la paroi entre ces deux sciences, dont le propre est d'exprimer, précisément, ce qu'elles ont en commun.

  

En géométrie, toute figure pouvant être augmentée par croissance continue possède, par définition, un gnomon; le gnomon ainsi défini se réduisant à la notion même de croissance géométrique.

Parmi les structures gnomoniques les plus fréquemment étudiées figurent, outre les polygones et polyèdres, le cône, ainsi que diverses figures tridimensionnelles en formes de coquillages ou de cornes, qui sont des figures engendrées par le développement d'une spirale logarithmique.

Le gnomon géométrique, ou "gnomon euclidien", est donc un instrument privilégié pour explorer tous les problèmes de croissance ou d'augmentation, non seulement mathématiques, mais physiques, et l'étude mathématique de structures telles que la corne, le coquillage, a fait l'objet d'un traitement par le savant naturaliste D'arcy Thompson, dans son livre Forme et croissance. 

Certains pourraient nous objecter que la définition euclidienne est en accord avec un usage courant du mot gnomon, qui désigne un instrument d'astronomie fondé sur le principe de l'ombre portée. Mais cette objection ne résiste pas au simple examen de la tradition pythagoricienne. Ce n'est pas d'un tel instrument que nous parle Philolaos, lorsqu'il définit le gnomon comme matrice du nombre et paradigme de la connaissance, ou Philopon, lorsqu'il énonce que les gnomons sont les nombres impairs.

 

 

B. La théorie pseudo-pythagoricienne des « nombres figurés »

 

Bien qu'il soit habituel de considérer la théorie des nombres figurés comme appartenant au fond théorique de l'ancien pythagorisme, nous n'avons pu lire aucun argument capable de nous en convaincre. Tout ce que nous savons de l'histoire du pythagorisme, nous incite plutôt à penser le contraire. 

En premier lieu, cette théorie (qui n'est pas une théorie) est contredite, et prouvée non pertinente, par la véritable théorie mathématique du gnomon. Donc, même si ces spéculations étaient anciennes, elles ne pourraient être le fait que de pythagoriciens acousmatiques, qui n'avaient pas accès à la connaissance des véritables théorèmes. 

Dans cette théorie, les pythagoriciens auraient voulu "représenter" des nombres par des constellations de points; et, à côté des nombres "triangles" et "carrés", auraient ainsi défini toutes sortes de nombres semblables, pentagonaux, hexagonaux, etc.

 

Avec cette méthode, on définit ainsi des «  nombres triangles » : 1, 3, 6, 10, etc.

 

  

Des « nombres carrés » : 1, 4, 9, 16, etc

  

 

Ou encore des « nombres pentagonaux » : 1, 5, 12, 22, etc

 

 

 

Il en résulte une nouvelle définition du gnomon, selon laquelle le gnomon est la quantité de points qu'on ajoute, à chaque étape du processus, pour que la figure de base soit reconstituée.

  

 

On aperçoit toute de suite une différence fondamentale avec la théorie du gnomon. Dans cette dernière, on raisonne sur des constellations de points qui sont les centres des polygones considérés (triangles ou carrés), en accord avec la sentence classique : "une figure, un pas". Au lieu que, dans la théorie des nombres figurés, on raisonne sur des constellations de points qui sont les sommets des figures considérées. Il en résulte ce paradoxe immédiat :  que l'unité ne peut être considérée autrement que comme un nombre à la fois triangle, carré, pentagonal, etc, alors qu'elle n'est en réalité rien de tout cela, puisqu'elle est un point. Dans la théorie du gnomon, le paradoxe est absent. L'unité - ou atome - n'est pas un polygone "en puissance", mais une figure bien réelle : un triangle ou un carré. 

Mais le problème le plus grave de cette théorie, c'est qu'elle se résume à un jeu purement arithmétique, qui ne désigne aucune propriété géométrique pertinente des figures en question.

Le jeu dont il s'agit est équivalent à celui qui consiste à dire : que se passe-t-il si je dispose des boules aux quatre coins d'un carré, puis au milieu de chaque côté, puis au milieu de chacun des nouveaux segments délimités, et ainsi de suite. Le résultat obtenu ne contient pas d'information géométrique intéressante sur le carré,  puisqu’il résulte d'une règle purement arithmétique, qui marcherait tout aussi bien avec une figure en forme de ligne brisée comportant le même nombre de segments que le carré. De la même manière, dans la théorie des nombres figurés, les figures ne constituent, tout bien considéré, qu'un catalogue de représentations "graphiques" pour diverses formules de calcul, dont la substance est purement arithmétique, - catalogue qui ne présente donc pas d'ordonnance ni de raison systématique, faute de justification dans l'ordre mathématique de la symétrie, qui est  le seul dans lequel une théorie de ce genre pourrait consister.

En définitive, seuls les nombres triangles et carrés, qui sont ceux qui ont une réelle pertinence en terme de symétrie, puisqu'ils correspondent à des réseaux hexagonaux et orthogonaux réguliers, présentent aussi un intérêt pour la théorie du gnomon; mieux, on peut faire remarquer que la théorie du nombre figuré a formulé un principe qui n'est qu'une transformation de la loi du gnomon, à savoir : que deux nombres triangulaires successifs forment un nombre carré. 

En effet, on  a vu que tout polygone gnomonique de rang supérieur à un, triangle ou carré, était composé de deux "nombres triangulaires" successifs, c'est à dire de deux réseaux hexagonaux entrelacés, ou encore, de deux structures tétractyques démarrant avec un temps de décalage.

Comme il existe de nombreux sites internet ou ces jeux mathématiques sont abordés, on se dispensera de le faire ici, d'autant qu'ils n'ont, comme on le voit, presqu'aucun rapport avec la véritable théorie du gnomon.

Pour nous résumer, alors que le gnomon euclidien est une notion purement géométrique, sans contenu arithmétique, le gnomon de la théorie du nombre figuré, au contraire, est un jeu arithmétique, sans contenu géométrique pertinent, et dont l'intérêt mathématique peut en toute justice être comparé à celui d'une table de multiplication. Or, comme on l'a vu, la véritable théorie du gnomon n'appartient spécialement ni à l'arithmétique, ni à la géométrie, mais à l'exacte interface entre ces deux sciences, qui est la logique pythagoricienne.

 

Par chance, la tradition a conservé divers témoignages de l'ancienneté de la théorie exacte du gnomon.

On peut citer Aristote :

"Eurytos, pour sa part, attribuait un nombre à chaque chose, (...) comme on ramène les nombres aux figures du triangle et du carré." (Où il n'est pas question d'autres polygones).

Un témoignage encore plus décisif est celui de Jean Philopon, qui, dans son commentaire de la Physique d'Aristote, affirme que les anciens appelaient gnomons les nombres impairs. Autrement dit : G = I. On est loin d'Euclide; mais cette définition disqualifie également la théorie du nombre figuré, puisque, dans cette dernière, seuls les gnomons de la série des "nombres carrés" peuvent être appelés "impairs", les autres séries de gnomons n'ayant aucun rapport avec la série des impairs.

En complétant la proposition de Philopon (G = I) par l'indication donné par Aristote, selon laquelle les figures à prendre en considération pour la théorie du nombre, sont le triangle et le carré, on reconstitue la loi du gnomon : G (t) = G (c) = I.

Mais sans chercher aussi loin, rappelons-nous que les expressions "carré" et "cube" appliquées aux puissances 2 et 3 d’un nombre, transmises sans interruption, depuis l'ancien pythagorisme, par la tradition mathématique, ne s'expliquent, elles aussi, que dans le cadre de la théorie exacte du gnomon, - du moins, cette théorie est le seul cadre dans lequel elles s'explicitent parfaitement, sans paradoxe sur le statut de l'unité.

 

  

 

    

APPLICATIONS PHYSIQUES

 

  

Les applications physiques des quatre concepts majeurs de la mathématique pythagoricienne sont innombrables, au point que la "physicalité" pourrait apparaître, sous un regard superficiel, comme leur qualité la plus frappante. Une revue même succincte exigerait un livre entier. On se contentera donc de citer un ou deux exemples pour chacun d'eux.

 

  

a) La tétractys

 

Bien que la symétrie hexagonale qui est celle de la tétractys ne soit qu'un cas particulier de symétrie mathématique, correspondant notamment à l'un des six ordres cristallins, elle revêt, au point de vue pythagoricien, le statut de porte d'entrée dans le monde de la symétrie, de par son caractère de "première en naissance". Cette prééminence s'explique par le fait qu'elle peut être construite par la simple réplication de cercles, ou de sphères, de même diamètre, s'agglomérant les uns aux autres; le cercle et la sphère étant les figures les plus simples qui existent dans leur dimension respective. En effet, bien qu'ils appartiennent aux dimensions (pythagoriciennes) 3 et 4, le cercle et la sphère sont des objets plus simples que les polygones et polyèdres, puisqu'on peut tous deux les définir au moyen de deux points seulement, - au lieu que le premier des polygones nécessite trois points. Le niveau de simplicité du cercle et de la sphère est donc à mettre sur le même plan logique que celui du segment (dim 2), puisque c'est en effet par le segment qu'est leur diamètre (ou, au choix, leur rayon), que ces objets sont définis.*

 

Si, sur un plan, on met deux billes de même diamètre au contact l'une de l'autre, puis une troisième au contact des deux premières, on a déjà constitué la matrice d'un réseau hexagonal continu. D'où, en poursuivant, par agglutination, sur un côté quelconque du triangle originaire, on parvient à une tétractys.

  

L'opale, pierre qui était prisée dans l'antiquité, est constitué d'un réseau hexagonal de billes de silice impeccablement empilées.

 

  

 

Le flocon de neige et l'alvéole des abeilles sont des exemples bien connus de symétrie hexagonale. Le premier est du à la triangularité de la structure moléculaire de l'eau (H2O), le second, au principe d'"économie", ou principe du moindre espace, qu'adoptent spontanément les abeilles, lorsque, en un nombre quelconque, elles se répartissent sur la surface du morceau de cire pour y creuser leurs galeries par un vol rotatif : principe qui les détermine à se grouper en constellation hexagonale, aussi imparablement que les billes évoquées ci-dessus; la structure hexagonale de l'alvéole proprement dite résultant ensuite des lois de la tension superficielle, analogues à celle qui veut qu'une bulle de savon adopte spontanément une forme sphérique.

         

               

  

  

    

b) Les médiétés

 

Le cœur de la fleur de tournesol, comme celui de nombreuses autres fleurs (marguerite, pissenlit, artichaut), s’ordonne selon une règle arithmétique qui est celle d'une "suite de Fibonacci" tendant vers le nombre d’or (médiété Nicomaque 10).

 

   

c) Le Gnomon

 

"La croissance de la corne, de la coquille et de toute autre forme organique où se dessine une spirale est caractérisée par le fait que chaque incrément de la croissance est semblable au précédent, que sa taille et sa position sont semblables à celles de l'élément précédent, et qu'il constitue dès lors un gnomon de toute la structure préexistante."**

D'arcy Thompson

 

 

                                                                    

 

             

 

d) Les solides réguliers 

  

Les 5 solides réguliers furent recensés par Haeckel dans le monde des radiolaires, ces protozoaires pourvus d'un squelette siliceux, appartenant au plancton marin. Selon d'Arcy Thompson, ces structures semblent réalisées au moyen d'un maillage hexagonal. Le virus du rhume est un icosaèdre.

 

 

   

Après cet aperçu des applications physiques des concepts pythagoriciens, nous reviendrons, dans les deux articles suivants, sur la théorie du gnomon, pour montrer que le gnomon est une structure logique qui permet, notamment, de construire l'ensemble des axiomes et des applications de la logique moderne des tables de vérité.

  

    

* Comme nous le montrons ailleurs, le cercle, ou plus exactement le disque, et la sphère, ou plus exactement la boule topologique, peuvent même, d'un point de vue plus profond, être reconduits l'un et l'autre à la dimension 1, n'étant, au regard de l'unité arithmétique, qu'un point "étalé" pour l'un, et un point "gonflé" pour l'autre. Une bille est une monade, parce qu'elle n'est rien d'autre qu'un point "muri", déplié depuis sa dimension, qui, elle, reste toujours "repliée", indéfinie. (Voir : Monadologie, in Le développement continu de la tétractys).

** Le gnomon défini par D'arcy Thompson demeure, en raison de sa généralité, un gnomon géométrique; toutefois, certaines des structures évoquées ici, engendrées par le développement d'une spirale logarithmique, peuvent être construites au moyen de triangles ou de carrés gnomoniques, et ont ainsi pu recevoir une définition arithmétique rigoureuse (suites de Padovan et de Fibonacci). Ces structures relèvent, à la fois, de la théorie du gnomon et de celle des médiétés.  

  

  

  

 

   

LA STRUCTURE LOGIQUE DU GNOMON (I) 

Connecteurs binaires et carré logique

  

  

  

 Introduction

  

Si, d'une certaine manière, la mathématique toute entière peut être considérée comme une interface entre nombre et figure, la théorie du gnomon possède une particularité exclusive, qui est d'associer de façon biunivoque, et au niveau le plus fondamental, les notions de nombre entier et de figure entière. En effet, ce qui est en question dans cette théorie est un objet mathématique qui est précisément le nombre de figures. Le gnomon est le nombre de figures, que l'on doit ajouter à une figure, pour la reconstituer.

Dans cette théorie, "arithméticité" et "géométricité" se trouvent donc impliquées à parts égales; les gnomons sont des objets dont la nature est inséparablement, arithmétique et géométrique. Dans l'ordonnance de la science pythagoricienne, la théorie du gnomon ne peut donc pas, sans arbitraire, être rangée dans une de ces sciences plutôt que dans l'autre, et c'est pour cela qu'elle constitue le fondement d'une troisième.

Les gnomons possèdent, en premier lieu, les propriétés logiques qui sont celles d'un tableau. Ils présupposent, comme on l'a vu, les notions d'atome et de système. Mais ils possèdent aussi des propriétés structurelles plus profondes, au point d'apparaître comme des candidats au statut de notions centrales, fondatrices, de la logique mathématique. Dans ces deux derniers articles, l'enquête sera poussée un peu plus loin, et nous verrons que ces gnomons peuvent être traités comme de véritables blocs de logique pure; - nous verrons qu'ils permettent, en particulier, de retrouver un matériel équivalent à celui de la logique moderne des tables de vérité; le système de symétries qui se déploie dans l'espace du gnomon, étant, dans sa structure et sa forme, identique au système de différences qui caractérise cette logique des tables de vérité.

  

 

  

Le carré logique

 

Le carré gnomonique de rang 2, qui est un carré composé de 4 cases égales, peut être considéré comme un système de différence informationnelle. 

En effet, si l'on autorise, par exemple, pour toute case du carré gnomonique, 2 valeurs  ou "états" possibles - ici blanc ou noir - on obtient un système de différences combinatoires, constitué de 2⁴ = 16 possibilités qui sont les suivantes :

 

 

 

Mais avant d'aller plus loin dans l'examen de ce système, nous devons ouvrir une parenthèse pour présenter succinctement le principe de la logique des tables de vérité.

Pour le moment, on retiendra simplement que, dans cette étude, on appelle "carré logique" le système de différences combinatoires contenu dans un carré gnomonique de rang 2, lorsque chacune de ses cases a deux valeurs, ou deux états possibles - pour nous : "blanc" ou "noir".

 

 

  

La construction mathématique de la signification logique

 

La logique des tables de vérité est un système qui permet de créer des significations multiples et complexes, à partir de significations élémentaires plus simples, et peu nombreuses. Le moyen mis en oeuvre est celui de la combinatoire. Des significations logiques riches et diversifiées, telles que les notions de relation entre deux énoncés, du genre : "et", "ni, ni", "ou inclusif", "si et seulement si" (ces 4 éléments étant soustraits d'un ensemble qui en compte 16), sont "fabriquées" par la seule combinaison d'éléments de signification plus simples : les valeurs de vérité V et F (vrai et faux), les énoncés atomiques quelconques notés p et q, enfin la notion de relation combinatoire ou de connecteur binaire, entre deux énoncés p et q. 

La définition de ces notions élémentaires ne nécessite pas une extrême précision, dans la mesure où tout leur contenu réside, non en elles-mêmes, mais plutôt dans leur différence avec les autres, dans le système résultant de leur combinaison. Un texte court peut donc suffire à définir toutes ces notions, du fait de la solidarité de chacune avec les autres, en supposant que les constituants ultimes de la signification de mots tels que "vrai", "faux", "proposition", tombent suffisamment dans l'intuition.

 

Définitions :

 

"Un énoncé est une proposition qui a deux valeurs de vérité possibles : "vrai" ou "faux". Un connecteur binaire est une relation logique entre deux énoncés p et q, dont la valeur de vérité est connue pour toutes les valeurs de vérité possibles de p et de q."

Voyons maintenant le moyen par lequel des notions de relation complexes telles que "et", "ni, ni", peuvent être construites à partir d'éléments aussi réduits que ceux détaillés dans la définition ci-dessus.

Dans le système des tables de vérité, on ne considère les énoncés logiques que sous un unique aspect : le fait qu'ils soient vrais ou faux.

Autrement dit, la relation "et" signifie simplement que les énoncés p et q sont tous les deux vrais, la relation "ni, ni", que ni p ni q ne sont vrais, la relation "implique" se dit : "si p est vrai, alors q est vrai", etc.

A présent, pour être tout à fait complet, nous pouvons définir la relation "et" comme la relation qui est vraie lorsque p est vrai et q vrai, et qui est fausse dans tous les autres cas. Mais quels sont ces autres cas? Il y en a trois. Lorsque p est vrai et q faux; lorsque p est faux et q vrai; lorsque p et q sont tous les deux faux. Autrement dit, la relation "et" est la relation qui a pour "table de vérité" la séquence VFFF, qui signifie : "vrai dans le premier cas et faux dans les trois suivants".

On voit qu'il est facile, d'ores et déjà, de définir de cette manière la relation "ni, ni". En effet, la relation "ni, ni" est la relation qui a pour table de vérité la séquence FFFV, c'est-à-dire qu'elle est vraie dans le quatrième cas et fausse dans les trois premiers.

A la question : combien y a-t-il de "connecteurs" ou de relations binaires de ce genre? La réponse est : autant qu'il y a de façons possibles de remplir un diagramme de 4 cases avec les lettres V et F : il y en a donc 16.

Nous les exposons ci-dessous verticalement, en leur attribuant un numéro d'ordre qui ne s'expliquera que dans le prochain article, et que l'on demande au lecteur d'accepter pour le moment comme une convention arbitraire, et nous détaillons ensuite les significations de ces connecteurs en langage naturel, significations sur lesquelles nous reviendrons ensuite de façon plus détaillée. 

  

p

q

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

V

V

V

F

F

F

F

V

V

V

F

F

F

V

V

V

V

F

V

F

F

V

V

F

F

F

V

V

V

F

F

V

V

F

F

V

F

V

F

F

V

V

F

V

V

F

F

F

V

V

F

F

V

V

F

F

F

F

F

F

V

F

V

F

V

F

V

F

V

V

V

V

  

1 : VFFF : « et »

2 : FVFF : « contre-implique »

3 : FVVF : « ou exclusif »

4 : FFVF : « est contre-impliqué par »

5 : FFFV : « ni… ni… »

6 : VFVF : « q » ou « identité de q »

7 : VVVV : « toujours vrai »

8 : VVFF : « p » ou « identité de p »

9 : FFVV : « non p » ou « négation de p »

10 : FFFF : « toujours faux »

11 : FVFV : « non q » ou « négation de q »

12 : VVVF : « ou inclusif »

13 : VVFV : « est impliqué par »

14 : VFFV : « si et seulement si »

15 : VFVV : « implique »

16 : FVVV : « est incompatible avec »

 

 

On remarque que les 16 relations logiques entre deux énoncés p et q, les 16 connecteurs binaires, sont identiques aux 16 carrés logiques bicolores présentés en introduction.

 

En effet, si l'on convient qu'à la table de vérité d'un connecteur, composée des lettres V et F, et lue de gauche à droite selon la liste ci-dessus, correspond un carré logique lu dans cet ordre constant :

 

            1 2

            3 4

 

Et si l'on attribue à chaque valeur de vérité une couleur également constante, (par exemple : Vrai = Blanc; Faux = Noir), alors, il existe une application biunivoque qui attribue, à chacun des connecteurs du langage logique, un et un seul carré logique. Autrement dit : les carrés logiques ne sont rien d'autre que des noms logiques des connecteurs du système des tables de vérité.

 

*

 

Après avoir établi que les carrés logiques bicolores sont des noms logiques des relations - ou connecteurs - du système des tables de vérité, nous pouvons porter un regard vers le but de cet article, qui est de montrer que le contenu sémantique, que les significations de ces connecteurs, se reflètent, elles aussi, dans la structure matérielle des carrés logiques qui leur correspondent.

Pour le montrer, il nous faut pénétrer plus avant dans le contenu sémantique du système des tables de vérité.

 

  

 

Analyse du système sémantique

 

Les 16 connecteurs binaires se répartissent en deux classes logiques rigoureusement distinctes.

 

A) Les connecteurs binaires de sens binaire, au nombre de 10.

 

Ce sont, outre les relations "et" (1), et "ni… ni…" (5), déjà évoquées, dont l’intuition est assez évidente, un groupe de 4 : "implique" (15), "contre-implique" (2), "est impliqué par" (13), "est contre-impliqué par" (4), dont le sens logique rigoureux doit se construire à partir du premier : "implique" signifie "si p (est vrai), alors q (est vrai)". Pour les trois autres, on obtient : "si p alors non q", "si q alors p", "si q alors non p".

Quatre autres connecteurs : "ou exclusif" (qui signifie qu'entre les énoncés p et q, un seul est vrai) (3), "ou inclusif" (qui signifie qu'au moins l'un d'entre eux est vrai) (12), "si et seulement si" (14), "est incompatible avec" (16).

 

 

B) Les connecteurs binaires de sens non binaire.

           

Cette classe se divise à son tour en deux sous-classes.

 

a) Les connecteurs unaires, au nombre de 4.

 

Ce sont des connecteurs dont les tables de vérité n’énoncent pas autre chose que "p" (8), "non p" (11), "q" (6) et "non q" (9).

Si, dans le connecteur pRq dont la table de vérité énonce "p", il y a bien une sorte de relation entre p est q, cette relation n’est autre que l’identité de p avec lui-même. pRq est ici la relation de p avec q qui laisse p inchangé, identique à lui-même.

Ces connecteurs sont donc en réalité des connecteurs unaires; et il n’existe que deux connexions unaires : l’identité et la négation - ici, l’identité et la négation de p et de q.

 

 

b) Les connecteurs nuls

 

Enfin, deux connecteurs, dont les tables de vérités sont VVVV (7) et FFFF (10), qu’on a coutume de qualifier de saturés ou de dégénérés, parce qu’ils n’ont réellement aucun sens logique. Une proposition pRq, qui serait vraie quelle que puisse être la vérité de p et de q, n’a réellement aucun contenu logique intuitif.

Comme tels, ces connecteurs ne font qu’énoncer les pièces de construction du système, le "toujours vrai" et le "toujours faux", entre lesquelles s’établissent les expressions ayant un contenu logique (vrai - ou faux - si...).

 

  

Le plein et le vide logiques

 

Parmi toutes les différences (qui sont les caractères constituants de la signification logique) que l'on peut voir se manifester ici, l'une est plus importante que les autres, c'est celle du plein et du vide logiques.

En quoi consiste précisément cette différence?

Les 16 connecteurs sont binaires au point de vue formel. Mais au point de vue sémantique, 6 sont binairement "vides" (classe B), tandis que 10 sont binairement "remplis", - remplis d'un sens, d'une signification binaire (classe A). 

Or que constate-t-on? Les 6 connecteurs binairement vides ne sont autres que les pièces de construction de la signification, les constituants ultimes de la sémantique du système, à savoir les deux valeurs de vérité V et F, désignées par les connecteurs saturés (VVVV), (FFFF), et les énoncés quelconques p et q, avec leurs négations, non p et non q, exprimant certes des connexions, mais de nature non binaire mais unaire : l'identité et la négation.

Autrement dit, il y a identité entre la structure du système, et le vide de celui-ci, en ce sens que les formules "échouées" ou "non réalisées" du système, - ses formes vides, ne sont autres que les pièces nécessaires à sa construction.

 

Les significations des connecteurs se reflètent dans la structure matérielle du carré logique.

 

Il nous faut maintenant remarquer qu'il existe une relation tout à fait structurelle et profonde, entre la nature de la connexion logique entre deux énoncés p et q (binaire, unaire ou nulle), pour un connecteur quelconque, et le nombre d'axes de séparation entre les domaines respectifs des lettres V et F (des couleurs blanc et noir), sur le carré logique correspondant au même connecteur.

Autrement dit :

- Les connecteurs binaires ont deux axes de séparation, qui sont la verticale et l’horizontale.

- Les connecteurs unaires n’ont qu’un axe de séparation : la verticale ou l’horizontale.

- Les connecteurs nuls n’ont aucun axe de séparation.

 

                 connecteurs binaires              connecteurs unaires                 connecteurs nuls

   

Non seulement les carrés logiques sont des noms logiques des connecteurs du système des tables de vérité, mais on voit ici que le contenu sémantique, que les significations de ces connecteurs, se reflètent dans la structure du carré logique. 

De la même manière que la tétractys à points triangulaires, comme on l'a vu dans notre article 1 consacré à l'arithmétique, est un système de coordonnées qui permet de repérer de façon biunivoque l'ensemble des nombres entiers, mais aussi des nombres décimaux et négatifs, les carrés logiques bicolores constituent un système de notation capable d'exprimer l'ensemble des propositions de la logique des tables de vérité.

  

 

Théorème de consistance du carré logique 

 

La puissance exceptionnelle de ce système résulte, semble-t-il, d'une autologie bien construite, grâce à laquelle les couleurs, ou autres valeurs du carré logique, acquièrent la valeur de noms d'elles-mêmes. En effet, si l'on remplace les couleurs "blanc" et "noir" par les deux catégories primordiales de la logique : Identité et Différence, on obtient un système autologique consistant et bien construit (sans paradoxe) : c'est-à-dire un système qui formule lui-même les conditions minimales de sa propre possibilité. En effet, si le blanc n'était pas identique au blanc, et si le noir n'était pas différent du blanc, il serait impossible de construire un carré logique avec du blanc et du noir; - ces deux conditions suffisant à définir complètement ce qui est nécessaire à ces deux couleurs pour leur permettre de figurer ensemble dans un carré logique. De la même manière exactement, si l'expression "Identique à soi-même" n'était pas identique à elle-même, et si l'expression : "Différent de l'autre" n'était pas différente de l'autre, il serait impossible de construire un carré logique avec les expressions "Identique à soi-même" et "Différent de l'autre". Ce que l'on peut aussi exprimer par : Si ces expressions ne possédaient pas elles-mêmes la propriété qu'elles énoncent, il serait impossible de construire un carré logique avec elles.  Conclusion : le système énonce réellement les conditions minimales, nécessaires et suffisantes, de sa propre possibilité; et les valeurs du carré logique sont des désignations correctes d'elles-mêmes; ou encore : chacune de ces expressions stipule réellement, et sans paradoxe, ce qu'elle est elle-même. 

  

Identique à soi-même	Différent    de l'autre

             

Enfin, le carré logique est consistant pour toute paire d'objets (a, b) - valeurs ou états des cases du carré logique - satisfaisant ensemble à ces propriétés. Notons que la valeur "b" du carré logique n'a pas besoin, quant à elle, d'être identique à elle-même, pour peu que la valeur "a" le soit. Ainsi, si la valeur "a" est représentée par la couleur blanche, la valeur "b" peut être représentée par 32 couleurs différentes, voire 32 écrans versicolores, pourvu que toutes ces couleurs, ou tous les états de ces écrans, soient différents du blanc

  

*

  

Par ce chemin, la logique des tables de vérité, construite par la combinaison des valeurs de vérité "vrai" et "faux", se voit subordonnée à un matériel logique d'une généralité supérieure - dont elle apparaît comme un simple cas particulier - qui est celui des catégories primordiales de l'Idendité et de la Différence : le Même et l'Autre du Timée de Platon.

La logique des tables de vérité est intéressante par sa façon d'occuper (voire d'envahir, étant donnée sa dimension incontestable de conquête intellectuelle) ⁽¹⁾ un espace logique qui  peut être occupé par bien d'autres objets que le vrai et le faux : des couleurs, des sons, ou encore un circuit électronique capable d'effectuer des calculs. Mais on peut affirmer qu'il est impossible de "remplir" cet espace logique avec un matériel qui ait plus de généralité, ou d'extension, (et donc moins de contenu ou de déterminité ontologique) que les deux expressions ci-dessus, puisque les propriétés que ces expressions désignent et possèdent à la fois, sont des propriétés que possèdent nécessairement toutes les paires d'objets qu'il soit possible de poser, ou de définir, dans un carré logique consistant. Ou encore : le carré logique est consistant si et seulement si la paire d'objets qui le compose, est dotée de ces propriétés.

A nos yeux, c'est donc bien le carré logique, - et à travers lui son cadre vide : le carré gnomonique de rang 2 - qui apparaît dans cette application comme l'opérateur mathématique le plus fondamental, en ce qu'il permet de subordonner, par une méthode qui est réellement analytique et complète, une catégorie logique à une autre, en l'occurrence la catégorie "Vrai-Faux" à la catégorie "Identité-Différence". Plus précisément encore, le carré logique est l'opérateur dont ces catégories logiques sont les objets résultants.   

 

 

⁽¹⁾ Comme l'invention pythagoricienne de la théorie musicale, la logique des tables de vérité est, en réalité, l'une des plus hautes conquêtes intellectuelles de la science mathématique. Chacune de ces inventions représente l'intégration par la mathématique d'un pan entier de l'expérience humaine : la musique dans le premier cas, la logique dans le second. Pourtant, malgré le développement extraordinaire de la logique et de l'informatique au XXe siècle, le logicien Boole, son inventeur, n'est pas devenu, autant que nous sachions, une "icône de la modernité", à l'inverse des glorieux fabricants de machines qui ont prospéré sur le terreau de son invention. Les inventions de ce genre sont en quelque sorte victimes de leur succès, en ce qu'elles s'intègrent si vite et si naturellement au paysage culturel de l'homme, qu'on oublie de les remarquer, alors même que, du fait de leur appartenance au paradis des mathématiques, elles sont éternelles, - contrairement aux théories physiques incomplètes et provisoires auxquelles le public accorde sa faveur. De notre point de vue, il n'y a rien, dans la théorie des ensembles, qui ne puisse être déduit par un biais ou un autre de la logique des tables de vérité; et cette théorie se serait épargnée bien des ennuis si elle avait choisi, dès le départ, d'adhérer à ce socle, pour ne pas le quitter.

 

  

 

  

 LA STRUCTURE LOGIQUE DU GNOMON (2)

  Le système des connecteurs et le triangle gnomonique de rang 4

 

  

 

Dans le précédent article, on a vu que les carrés logiques bicolores étaient des noms logiques des connecteurs du système des tables de vérité; mais on a constaté aussi que le contenu sémantique, que les significations de ces connecteurs, se reflétaient dans la structure matérielle du carré logique.

Dans cet article, on examinera une application de rang supérieur qui est la suivante :

Les relations logiques entre les 16 connecteurs de la logique des tables de vérité, se reflètent dans la structure des polygones gnomoniques de rang 4, triangle et carré. 

Ce qui, dans le système des tables de vérité, s'exprime par des relations de négation ou de réciprocité logique entre des connecteurs considérés par paires, se reflète dans la structure des polygones gnomoniques de rang 4, exprimé cette fois sous la forme de relations de symétrie - "haut-bas" ou "gauche-droite" - entre deux parties de la figure.

Autrement dit : A toute relation de négation ou de réciprocité entre deux connecteurs de la logique des tables de vérité, correspond une relation de symétrie entre deux cases du polygone gnomonique de rang 4, triangle ou carré.

En logique, les différences et les symétries d'un système s'articulent en un noyau logique, qui détermine la constitution, - la structure même - de ce système.

Rappelons-nous le noyau logique de différences et de symétries qui caractérise le système des connecteurs binaires. 

5 connecteurs de sens binaire s'opposent à 5 autres qui sont leurs négatifs. 3 connecteurs de sens non binaire s'opposent à 3 autres qui sont leurs négatifs. Précisons que, pour ce qui nous concerne, le choix de baptiser "positif" le groupe supérieur correspondant aux connecteurs 1 à 8, relève d'une convention arbitraire; en effet, un connecteur n'est pas en lui-même positif ou négatif, mais il est en lui-même le négatif d'un autre connecteur.

Par convention, donc, un groupe de 8 connecteurs appelés positifs, composé de 5 binaires et de 3 non binaires, s'oppose à un groupe de 8 autres connecteurs qui sont les négatifs des premiers cités, composé lui aussi de 5 binaires et de 3 non binaires. 

 

 

Ce système de différences peut être synthétisé dans le schéma géométrique suivant (constellation de points en réseau orthogonal) :

 

            1           2          3          4          5

            *          *          *          *          *

                       8           7          6          

                        *          *          *

                       9         10         11

                        *          *          *

           16         15        14         13         12             

            *          *          *          *          *

 

Où la moitié supérieure de la structure représente l'ensemble positif (connecteurs 1 à 8), et la moitié inférieure l'ensemble négatif (connecteurs 9 à 16); tandis que la partie intérieure de la structure représente l'ensemble des six connecteurs non binaires, et sa partie extérieure, l'ensemble des dix connecteurs binaires. 

Dans ce schéma topologique, la relation de symétrie entre le haut et le bas de la structure est la relation de négation logique. Les connecteurs du bas de la structure sont la négation des connecteurs du haut. Tandis que la relation entre la gauche et la droite de la structure est la relation de réciprocité logique. Par exemple, la relation « implique » (15) est la réciproque de la relation « est impliqué par » (13); la relation « et » (1) est la réciproque de la relation « ni, ni » (5). Quant à l’axe de symétrie vertical de la structure, il est constitué des quatre connecteurs qui n'ont pas de réciproque.

Il n'est pas difficile de s'apercevoir que, par une déformation convenable, cette structure constitue le plan de construction d'un triangle gnomonique de rang 4.

  

  

Si l'on examine le plan de construction, représenté ci-dessus par le développement de la chaîne des nombres 1 à 16, on remarque qu'il se conforme aux règles conventionnelles suivantes :

 

1- La chaîne se développe sans rupture de continuité.

2- Le passage d'un "maillon" au suivant s'effectue par une rotation de 180 degrés du triangle originaire, numéroté 1, soit sur l'un de ses sommets, soit sur l'un de ses côtés, autour d'un axe quelconque du plan, de façon qu'un seul triangle soit en mesure de construire la figure complète par un mouvement rotatif ininterrompu, et intégralement coordonné, dans l'espace euclidien.

3- Le point d'arrivée (16) rejoint le point de départ (1), de façon que la chaîne soit fermée.

4- Le sens de lecture principal de la chaîne, qui est déterminé par son origine, se déroule de gauche à droite, puis du haut en bas de la structure.

5- Le point de départ de la chaîne se situe à gauche de la structure.

           

Par une déformation convenable de la structure qui est celle de la construction du triangle, on constate qu'elle se transforme en celle de notre constellation orthogonale, de sorte qu'à chacune des symétries du système des connecteurs correspond une symétrie bien réelle du triangle, qui fait correspondre 8 triangles à 8 autres au sein d'une relation biunivoque.

 

 

Dans cette application, à chacun des quatre étages, ou lignes, de notre constellation orthogonale, correspond une séquence de la construction du triangle gnomonique de rang 4.

Nous pouvons déjà remarquer que, dans le triangle gnomonique, un "bloc positif" (regroupant nos 8 connecteurs positifs) s'oppose à un bloc négatif, dans une relation où chaque objet possède un correspondant exclusif, le hasard voulant que soit ici appelé "positif" le pôle "femelle" de la structure, et "négatif" le pôle "mâle", contrairement à l'usage qui est le plus fréquent en mécanique.

 

 

bloc (ou pôle) positif           

 

bloc (ou pôle) négatif

  

Notons encore que, du fait de notre convention de numérotation des connecteurs de 1 à 16, si l'on additionne le numéro d'ordre d'un connecteur avec celui de son négatif logique, la somme est toujours égale à 17, le nombre 17 étant le "zéro logique" du système de numérotation.

 

          1          2          3          4          5                               6          7          8

            +          +          +          +          +                              +          +          +

            16        15        14         13        12                           11        10         9

            =          =          =          =          =                              =          =          =

            17        17        17         17        17                             17        17        17

 

Les relations arithmétiques entre les numéros d'ordre des connecteurs correspondent aux relations géométriques entre les points de la chaîne de construction. 

 

 

 

Topologie de la séquence de construction : les différences et les symétries correspondent à des inversions du vecteur de lecture.

 

Si nous reprenons la structure de notre constellation orthogonale, nous constatons que les changements logiques qui s'opèrent, dans le système des connecteurs, lors du passage d'un étage à un autre, correspondent, dans la séquence de construction du triangle, à une inversion du vecteur de lecture de la chaîne des nombres.

 

 

Ligne 1 : 5 connecteurs binaires positifs (connecteurs 1 à 5)

lecture : "gauche-droite"

 

Ligne 2 : 3 connecteurs non binaires positifs (connecteurs 6 à 8)

lecture : "droite-gauche"

 

Ligne 3 : 3 connecteurs non binaires négatifs (connecteurs 9 à 11)

lecture : "gauche-droite"

 

Ligne 4 : 5 connecteurs binaires négatifs (connecteurs 12 à 16)

lecture : "droite-gauche"

 

Les italiques indiquent la variable qui a changé à chaque "saut de ligne", et auquel correspond l'inversion du vecteur de lecture. On peut remarquer que ce système est logiquement continu, en ce sens que les relations de négation du second degré y sont toutes également respectées. 

Ainsi, la ligne 1 est le négatif logique de la ligne 4, et leur vecteurs sont inverses.

La ligne 2 est le négatif logique de la ligne 3, et leurs vecteurs sont également inverses.

Enfin, les lignes qui ont le même vecteur de lecture, à savoir les lignes 1 et 3 d'une part, et 2 et 4 d'autre part, sont des lignes séparées par une double négation logique, double négation qui correspond bien logiquement à l'identité.

La totalité des relations de négation binaire de notre constellation orthogonale (qui est celle du système des connecteurs) se trouve donc exprimée, de façon continuellement logique, par la mise en oeuvre d'un vecteur de lecture à orientation binaire, qui n'est autre, rappelons-le, que celui même de la construction d'un triangle gnomonique de rang 4.

A ce sujet, précisons un point important. Le vecteur de lecture "gauche-droite" qui pourrait, en première approximation, apparaître imprécis ou vaseux dans la construction du triangle gnomonique, est bien évidemment une réalité mathématique exacte, résultant du calcul vectoriel, dès lors qu'on définit ce vecteur comme celui reliant le point de départ au point d'arrivée de chaque ligne (ou étage) du diagramme.

   

  

Entre le point 1 et le point 5, on s'est déplacé selon un vecteur qui est rigoureusement "gauche-droite", quel que soit le détour effectué en chemin, et ceci est valable pour chacune des 4 lignes de notre diagramme. L'opération logique qui permet cette simplification vectorielle exacte n'est autre que le saut de ligne distinguant les différents étages de la structure.

En résumé, l'ensemble des relations d'opposition binaire (négation ou réciprocité) du système de la logique des connecteurs, se retrouve dans la structure d'un triangle gnomonique de rang 4. A chacune des relations de négation ou de réciprocité entre deux connecteurs, correspond, de façon biunivoque, une relation de symétrie ("haut-bas", ou "gauche-droite") entre deux parties du triangle gnomonique.

 

Le triangle gnomonique de rang 4 n'est autre que la tétractys à points triangulaires, dont on a déjà vu, au début de cet exposé, qu'elle contenait un système de coordonnée biunivoque de l'ensemble des nombres entiers, mais aussi des nombres décimaux et négatifs.

 

Finissons par une dernière remarque structurelle.

On se souvient que, dans le système des tables de vérité, il existe une opposition essentielle entre les dix connecteurs de sens binaire qui sont les formes accomplies ou remplies du système, et les 6 connecteurs de sens non binaire, qui correspondent aux formes échouées ou vides, mais aussi à la structure profonde, c'est à dire aux constituants sémantiques de celui-ci.

Dans le triangle gnomonique de rang 4, les dix connecteurs binaires correspondent tout simplement aux 10 points de la tétractys, qui sont ceux d'une constellation hexagonale, tandis que les 6 connecteurs non binaires correspondent aux 6 interstices, logiquement vides, de cette structure, qui forment le départ d'une seconde tétractys, démarrant avec un temps de décalage, et composée de triangles orientés en sens inverse des premiers.

C'est-à-dire que l'opposition fondamentale du plein et du vide logique qui est définie combinatoirement dans le système des tables de vérité, se retrouve - ou n'est autre - que celle même, du plein et du vide logique de la tétractys à points triangulaires.

 

 

connecteurs binaires

 

connecteurs non binaires

  

  

 

Le carré gnomonique

 

En appliquant la loi de transformation du triangle en carré, le triangle gnomonique de rang 4 se transforme en carré gnomonique de rang 4. Alors que, dans le triangle gnomonique, toutes les relations de symétrie s'organisaient autour d'un axe qui est la médiatrice verticale du triangle, dans le carré gnomonique correspondant, les mêmes relations de symétrie entre les connecteurs s'organisent autour de sa diagonale, sur l’axe de laquelle on retrouve les centres des quatre séquences ou « brins » qui étaient ceux de la construction du triangle gnomonique. Les deux classes de connecteurs, binaires et non binaires, se retrouvent en situation d'opposition polaire. Les 10 connecteurs binaires se répartissent dans le coin en haut à gauche de la structure, et les 6 connecteurs non binaires dans le coin en bas à droite.

   

        axe de symétrie

           connecteurs binaires

  

connecteurs non binaires

  

En conclusion, les deux systèmes : gnomon d'un polygone, et logique des connecteurs, correspondent par une interface qui est celle de la structure logique; et cette correspondance se manifeste, en premier lieu, par la coïncidence de leurs cycles de clôture. De même qu'il faut et il suffit d'un carré de 4 cases, pour désigner l'ensemble des connecteurs de la logique des tables de vérité, de même, il faut et il suffit d'un polygone gnomonique de rang 4, triangle ou carré, pour exprimer l'ensemble des relations logiques détaillées existant entre ces connecteurs.